#Note to reader

This page contains an output log for analysis. Please contact Sam Rowe () if you have questions.






Evaluate Data

Load data

library(dplyr)
load(file="Baseline.Rdata")
load(file="SDCTCOW.Rdata")
load(file="SDCTCOWDHI.Rdata")

SDCTCOW = SDCTCOW %>%
  mutate(Tx = recode(SDCTCOW$Tx,
                     "0" = "Blanket", "1" = "Culture", "2" = "Algorithm"))




Import file BL (cows included for analysis) for descriptive statistics

library(readr)
head(Baseline)




Inspect data

print(summarytools::dfSummary(Baseline, valid.col=FALSE, graph.magnif=0.5, varnumbers=F,style="grid"))
## Data Frame Summary  
##   
## Dimensions: 4704 x 15  
## Duplicates: 0  
## 
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | Variable     | Stats / Values             | Freqs (% of Valid)   | Graph                      | Missing |
## +==============+============================+======================+============================+=========+
## | FARMID       | Mean (sd) : 4 (1.5)        | 1 :  296 ( 6.3%)     | I                          | 0       |
## | [numeric]    | min < med < max:           | 2 :  324 ( 6.9%)     | I                          | (0%)    |
## |              | 1 < 4 < 7                  | 3 : 1044 (22.2%)     | IIII                       |         |
## |              | IQR (CV) : 2 (0.4)         | 4 : 1452 (30.9%)     | IIIIII                     |         |
## |              |                            | 5 :  948 (20.2%)     | IIII                       |         |
## |              |                            | 6 :  188 ( 4.0%)     |                            |         |
## |              |                            | 7 :  452 ( 9.6%)     | I                          |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | CowID        | Mean (sd) : 4575.5 (3181)  | 1116 distinct values |     :                      | 0       |
## | [numeric]    | min < med < max:           |                      | : : :                      | (0%)    |
## |              | 6 < 4298 < 23096           |                      | : : :                      |         |
## |              | IQR (CV) : 4152.5 (0.7)    |                      | : : :                      |         |
## |              |                            |                      | : : : :   . .              |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | QTR          | 1. LF                      | 1176 (25.0%)         | IIIII                      | 0       |
## | [factor]     | 2. LR                      | 1176 (25.0%)         | IIIII                      | (0%)    |
## |              | 3. RF                      | 1176 (25.0%)         | IIIII                      |         |
## |              | 4. RR                      | 1176 (25.0%)         | IIIII                      |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | Tx           | 1. 0                       | 1568 (33.3%)         | IIIIII                     | 0       |
## | [factor]     | 2. 1                       | 1592 (33.8%)         | IIIIII                     | (0%)    |
## |              | 3. 2                       | 1544 (32.8%)         | IIIIII                     |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | Spectramast  | 1. n                       | 1740 (37.0%)         | IIIIIII                    | 0       |
## | [character]  | 2. y                       | 2964 (63.0%)         | IIIIIIIIIIII               | (0%)    |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | Age          | Mean (sd) : 46.7 (15.2)    | 663 distinct values  | :                          | 0       |
## | [numeric]    | min < med < max:           |                      | :                          | (0%)    |
## |              | 30.4 < 44.4 < 122.3        |                      | : :                        |         |
## |              | IQR (CV) : 22.4 (0.3)      |                      | : : .                      |         |
## |              |                            |                      | : : : : : .                |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | Parity       | 1. 1                       | 2008 (42.7%)         | IIIIIIII                   | 0       |
## | [factor]     | 2. 2                       | 1420 (30.2%)         | IIIIII                     | (0%)    |
## |              | 3. 3                       | 1276 (27.1%)         | IIIII                      |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | IMIDO        | Min  : 0                   | 0 : 3164 (74.6%)     | IIIIIIIIIIIIII             | 462     |
## | [numeric]    | Mean : 0.3                 | 1 : 1078 (25.4%)     | IIIII                      | (9.82%) |
## |              | Max  : 1                   |                      |                            |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | DOSCC        | Mean (sd) : 4.4 (1.2)      | 395 distinct values  |       :                    | 0       |
## | [numeric]    | min < med < max:           |                      |     . : :                  | (0%)    |
## |              | 1.6 < 4.3 < 8.6            |                      |     : : : .                |         |
## |              | IQR (CV) : 1.6 (0.3)       |                      |   : : : : : .              |         |
## |              |                            |                      | . : : : : : : : .          |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | DOMY         | Mean (sd) : 27.3 (8.7)     | 87 distinct values   |             :              | 0       |
## | [numeric]    | min < med < max:           |                      |           : :              | (0%)    |
## |              | 1.8 < 28.6 < 49.4          |                      |         : : : .            |         |
## |              | IQR (CV) : 10.9 (0.3)      |                      |       . : : : :            |         |
## |              |                            |                      | . : : : : : : : .          |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | DODIM        | Mean (sd) : 324.7 (45.6)   | 179 distinct values  |   :                        | 0       |
## | [numeric]    | min < med < max:           |                      |   :                        | (0%)    |
## |              | 252 < 305.5 < 584          |                      |   :                        |         |
## |              | IQR (CV) : 49 (0.1)        |                      |   : .                      |         |
## |              |                            |                      |   : : : . .                |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | PrevCM       | 1. 0                       | 4056 (86.2%)         | IIIIIIIIIIIIIIIII          | 0       |
## | [factor]     | 2. 1                       |  648 (13.8%)         | II                         | (0%)    |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | PrevSCCHI    | Mean (sd) : 5.4 (1.3)      | 611 distinct values  |     . :                    | 0       |
## | [numeric]    | min < med < max:           |                      |     : : : .                | (0%)    |
## |              | 2.9 < 5.3 < 9.2            |                      |   : : : : :                |         |
## |              | IQR (CV) : 1.8 (0.2)       |                      |   : : : : : : .            |         |
## |              |                            |                      | : : : : : : : : . .        |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | DPlength     | Mean (sd) : 55.8 (7.8)     | 54 distinct values   |         :                  | 0       |
## | [numeric]    | min < med < max:           |                      |         :                  | (0%)    |
## |              | 30 < 56 < 87               |                      |         : :                |         |
## |              | IQR (CV) : 8 (0.1)         |                      |       : : :                |         |
## |              |                            |                      |   . : : : : : .            |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+
## | PCSampDIM    | Mean (sd) : 5.8 (2.8)      | 14 distinct values   |       :                    | 280     |
## | [numeric]    | min < med < max:           |                      |       :     :              | (5.95%) |
## |              | 0 < 6 < 13                 |                      |     . : . . :              |         |
## |              | IQR (CV) : 4 (0.5)         |                      | .   : : : : :              |         |
## |              |                            |                      | : : : : : : : : . .        |         |
## +--------------+----------------------------+----------------------+----------------------------+---------+




Descriptive statistics of subjects at enrollment

Comparison of demographics for each treatment group at dry-off

library(table1)
table1(~ Age + DOMY + DOSCC + PrevSCCHI + factor(PrevCM) + factor(Parity) | Tx, data=Baseline)
0
(n=1568)		 1
(n=1592)		 2
(n=1544)		 Overall
(n=4704)
Age
Mean (SD) 47.2 (14.6) 46.9 (15.9) 46.1 (15.0) 46.7 (15.2)
Median [Min, Max] 44.7 [30.8, 104] 44.1 [30.4, 111] 44.5 [30.4, 122] 44.4 [30.4, 122]
DOMY
Mean (SD) 26.7 (8.87) 27.9 (8.81) 27.3 (8.38) 27.3 (8.70)
Median [Min, Max] 27.7 [4.54, 49.4] 29.0 [1.81, 49.4] 29.0 [2.72, 49.4] 28.6 [1.81, 49.4]
DOSCC
Mean (SD) 4.45 (1.21) 4.38 (1.23) 4.45 (1.22) 4.43 (1.22)
Median [Min, Max] 4.33 [1.61, 8.35] 4.23 [1.61, 8.59] 4.39 [1.61, 8.25] 4.32 [1.61, 8.59]
PrevSCCHI
Mean (SD) 5.37 (1.30) 5.49 (1.23) 5.40 (1.29) 5.42 (1.28)
Median [Min, Max] 5.23 [2.87, 9.21] 5.37 [3.14, 9.21] 5.30 [2.94, 9.21] 5.30 [2.87, 9.21]
factor(PrevCM)
0 1344 (85.7%) 1360 (85.4%) 1352 (87.6%) 4056 (86.2%)
1 224 (14.3%) 232 (14.6%) 192 (12.4%) 648 (13.8%)
factor(Parity)
1 616 (39.3%) 732 (46.0%) 660 (42.7%) 2008 (42.7%)
2 516 (32.9%) 416 (26.1%) 488 (31.6%) 1420 (30.2%)
3 436 (27.8%) 444 (27.9%) 396 (25.6%) 1276 (27.1%)




Descriptive statistics of subjects at dry-off

Note that this table excludes cows (n=32) that were not included cow-level analysis (eg. cows with long or short dry periods).

table1(~ Age + DOMY + DPlength + DOSCC + PrevSCCHI + PrevCM + Parity | Tx, data=SDCTCOW)

Blanket
(n=407)		 Culture
(n=410)		 Algorithm
(n=394)		 Overall
(n=1211)
Age
Mean (SD) 47.5 (15.0) 47.2 (16.2) 46.3 (15.1) 47.0 (15.4)
Median [Min, Max] 44.8 [30.8, 114] 44.4 [30.4, 119] 44.6 [30.4, 122] 44.5 [30.4, 122]
DOMY
Mean (SD) 26.8 (8.88) 28.0 (8.89) 27.3 (8.38) 27.4 (8.73)
Median [Min, Max] 27.7 [4.54, 49.4] 29.0 [1.81, 49.4] 29.0 [2.72, 49.4] 29.0 [1.81, 49.4]
DPlength
Mean (SD) 55.3 (7.89) 55.9 (7.61) 55.9 (8.16) 55.7 (7.88)
Median [Min, Max] 56.0 [33.0, 84.0] 56.0 [33.0, 84.0] 56.0 [30.0, 87.0] 56.0 [30.0, 87.0]
DOSCC
Mean (SD) 4.46 (1.22) 4.39 (1.22) 4.45 (1.21) 4.43 (1.22)
Median [Min, Max] 4.36 [1.61, 8.35] 4.23 [1.61, 8.59] 4.39 [1.61, 8.25] 4.33 [1.61, 8.59]
PrevSCCHI
Mean (SD) 5.40 (1.32) 5.50 (1.22) 5.40 (1.29) 5.43 (1.28)
Median [Min, Max] 5.23 [2.87, 9.21] 5.37 [3.14, 9.21] 5.30 [2.94, 9.21] 5.30 [2.87, 9.21]
PrevCM
0 350 (86.0%) 351 (85.6%) 345 (87.6%) 1046 (86.4%)
1 57 (14.0%) 59 (14.4%) 49 (12.4%) 165 (13.6%)
Parity
1 158 (38.8%) 185 (45.1%) 167 (42.4%) 510 (42.1%)
2 133 (32.7%) 108 (26.3%) 123 (31.2%) 364 (30.1%)
3 116 (28.5%) 117 (28.5%) 104 (26.4%) 337 (27.8%)
Groups appear to be well balanced before and after exclusions, indicating that randomization was successful, and that drop-out is unlikely to affect our assumption of exchangeability between treatment groups.





Comparison of herds

library(table1)
table1(~ Tx + Age + DOMY + DPlength + DODIM + DOSCC + PrevSCCHI + PrevCM + Parity | FARMID, data=SDCTCOW)
1
(n=76)		 2
(n=82)		 3
(n=263)		 4
(n=388)		 5
(n=242)		 6
(n=47)		 7
(n=113)		 Overall
(n=1211)
Tx
Blanket 28 (36.8%) 27 (32.9%) 93 (35.4%) 122 (31.4%) 81 (33.5%) 16 (34.0%) 40 (35.4%) 407 (33.6%)
Culture 27 (35.5%) 24 (29.3%) 87 (33.1%) 136 (35.1%) 84 (34.7%) 16 (34.0%) 36 (31.9%) 410 (33.9%)
Algorithm 21 (27.6%) 31 (37.8%) 83 (31.6%) 130 (33.5%) 77 (31.8%) 15 (31.9%) 37 (32.7%) 394 (32.5%)
Age
Mean (SD) 48.7 (16.0) 46.8 (14.3) 46.8 (13.4) 47.5 (16.7) 47.0 (15.9) 42.9 (11.2) 46.6 (16.2) 47.0 (15.4)
Median [Min, Max] 45.2 [30.6, 90.2] 44.6 [30.7, 95.7] 44.8 [30.4, 95.5] 44.6 [31.7, 122] 44.7 [30.4, 115] 43.7 [31.0, 82.6] 44.6 [31.0, 114] 44.5 [30.4, 122]
DOMY
Mean (SD) 23.0 (6.30) 26.6 (9.64) 29.5 (6.91) 30.3 (7.84) 19.6 (8.55) 30.7 (4.81) 30.6 (6.33) 27.4 (8.73)
Median [Min, Max] 22.7 [9.07, 38.1] 28.6 [2.72, 44.0] 30.4 [8.62, 47.6] 30.4 [2.72, 49.4] 20.0 [1.81, 39.9] 30.8 [16.8, 40.8] 30.8 [15.4, 48.5] 29.0 [1.81, 49.4]
DPlength
Mean (SD) 53.2 (11.8) 52.5 (5.63) 57.8 (6.39) 55.6 (6.49) 55.7 (8.16) 60.3 (7.19) 53.0 (10.6) 55.7 (7.88)
Median [Min, Max] 52.0 [32.0, 85.0] 53.0 [30.0, 63.0] 58.0 [35.0, 87.0] 56.0 [35.0, 74.0] 55.0 [35.0, 85.0] 60.0 [47.0, 84.0] 55.0 [33.0, 77.0] 56.0 [30.0, 87.0]
DODIM
Mean (SD) 346 (51.4) 334 (52.7) 314 (37.9) 325 (44.4) 329 (51.2) 328 (43.4) 321 (39.1) 325 (45.8)
Median [Min, Max] 326 [292, 584] 304 [293, 512] 293 [266, 475] 296 [283, 468] 308 [252, 512] 314 [258, 444] 307 [272, 476] 306 [252, 584]
DOSCC
Mean (SD) 4.54 (1.04) 4.08 (1.15) 4.00 (0.907) 4.47 (1.16) 5.18 (1.39) 4.34 (0.966) 3.91 (1.09) 4.43 (1.22)
Median [Min, Max] 4.61 [2.56, 7.59] 3.96 [2.30, 8.17] 3.98 [2.60, 6.68] 4.48 [1.61, 8.59] 5.13 [1.61, 8.35] 4.47 [2.56, 6.61] 3.78 [2.56, 7.38] 4.33 [1.61, 8.59]
PrevSCCHI
Mean (SD) 5.48 (1.31) 5.06 (1.31) 4.77 (1.08) 5.77 (1.20) 6.13 (1.11) 5.02 (0.927) 4.73 (1.17) 5.43 (1.28)
Median [Min, Max] 5.31 [3.43, 9.21] 4.78 [3.33, 9.21] 4.61 [2.87, 8.21] 5.65 [3.00, 9.21] 6.07 [3.40, 9.21] 5.09 [3.09, 7.06] 4.53 [2.94, 8.00] 5.30 [2.87, 9.21]
PrevCM
0 62 (81.6%) 81 (98.8%) 228 (86.7%) 337 (86.9%) 191 (78.9%) 46 (97.9%) 101 (89.4%) 1046 (86.4%)
1 14 (18.4%) 1 (1.2%) 35 (13.3%) 51 (13.1%) 51 (21.1%) 1 (2.1%) 12 (10.6%) 165 (13.6%)
Parity
1 31 (40.8%) 33 (40.2%) 92 (35.0%) 180 (46.4%) 104 (43.0%) 23 (48.9%) 47 (41.6%) 510 (42.1%)
2 15 (19.7%) 28 (34.1%) 95 (36.1%) 101 (26.0%) 73 (30.2%) 17 (36.2%) 35 (31.0%) 364 (30.1%)
3 30 (39.5%) 21 (25.6%) 76 (28.9%) 107 (27.6%) 65 (26.9%) 7 (14.9%) 31 (27.4%) 337 (27.8%)




Outcome 1: Clinical mastitis

Kaplan Meier curve & log rank test for clinical mastitis

library(gmodels)
CrossTable(SDCTCOW$Tx,SDCTCOW$CM,prop.c=FALSE,prop.t=FALSE,prop.chisq = FALSE)
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  1211 
## 
##  
##              | SDCTCOW$CM 
##   SDCTCOW$Tx |         0 |         1 | Row Total | 
## -------------|-----------|-----------|-----------|
##      Blanket |       348 |        59 |       407 | 
##              |     0.855 |     0.145 |     0.336 | 
## -------------|-----------|-----------|-----------|
##      Culture |       360 |        50 |       410 | 
##              |     0.878 |     0.122 |     0.339 | 
## -------------|-----------|-----------|-----------|
##    Algorithm |       346 |        48 |       394 | 
##              |     0.878 |     0.122 |     0.325 | 
## -------------|-----------|-----------|-----------|
## Column Total |      1054 |       157 |      1211 | 
## -------------|-----------|-----------|-----------|
## 
##

Kaplan Meier curve

library(survminer)
library(survival)

KM <- survfit(Surv(CMTAR, CM) ~ Tx, data = SDCTCOW)
ggsurvplot(KM, data = SDCTCOW,  title = "", pval = T, conf.int = F,risk.table.col = "Tx",risk.table = T, risk.table.y.text.col = TRUE , surv.plot.height = 5, legend.labs = c("Blanket","Culture","Algorithm"), tables.theme = theme_cleantable(), ggtheme = theme_bw())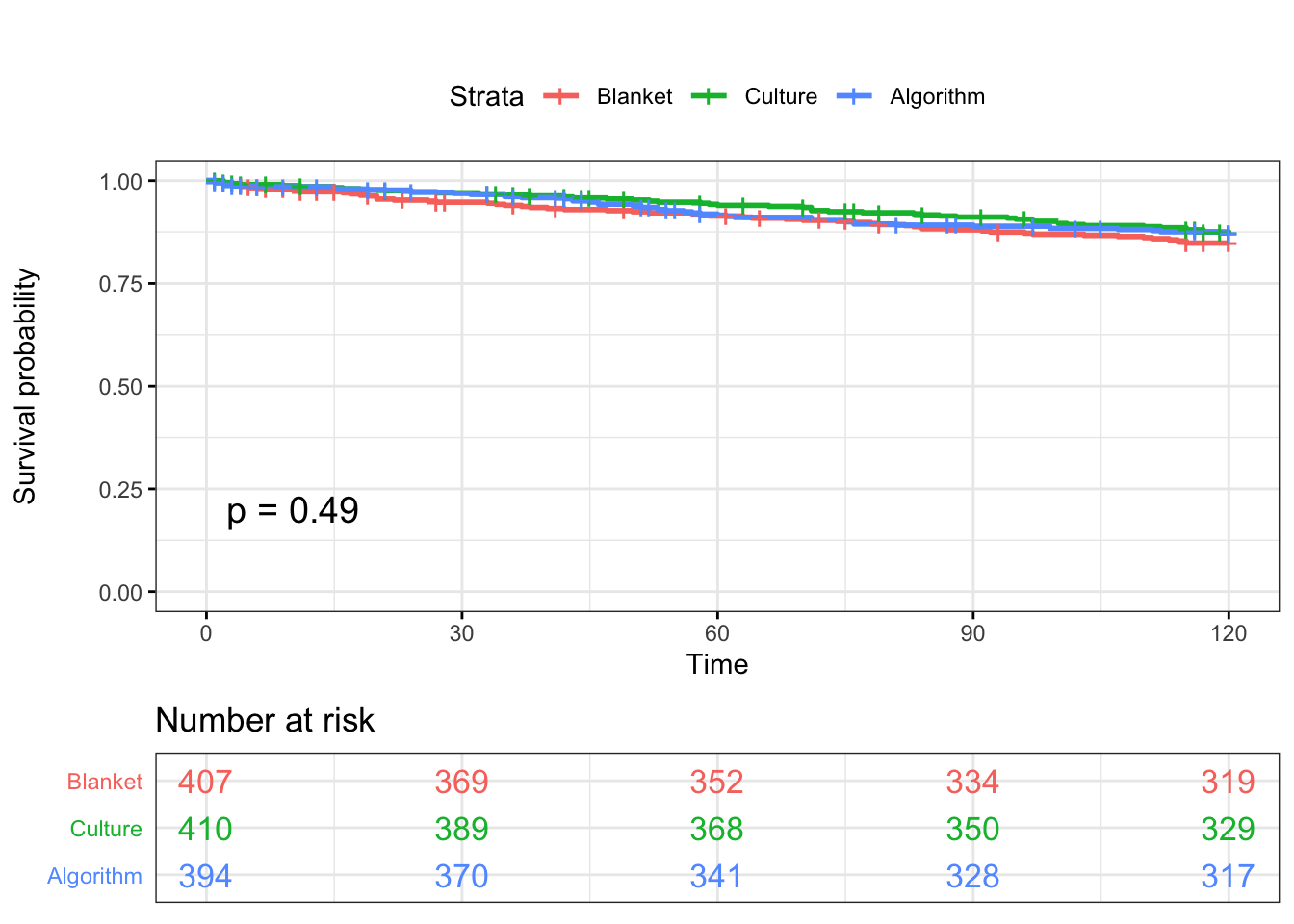





Log-Rank test

survdiff(Surv(CMTAR, CM) ~ Tx,data=SDCTCOW,rho=0)
## Call:
## survdiff(formula = Surv(CMTAR, CM) ~ Tx, data = SDCTCOW, rho = 0)
## 
##                N Observed Expected (O-E)^2/E (O-E)^2/V
## Tx=Blanket   407       59       52     0.954     1.428
## Tx=Culture   410       50       54     0.298     0.454
## Tx=Algorithm 394       48       51     0.180     0.267
## 
##  Chisq= 1.4  on 2 degrees of freedom, p= 0.5




Cox proportional hazards regression for clinical mastitis (1-120 DIM)

Model building plan

Model type: Cox proportional hazards analysis with farm included as a cluster variable (robust sandwich standard error estimator) to account for lack of indepedence.

Step 1: Identify potential confouders using a directed acyclic graph (DAG)

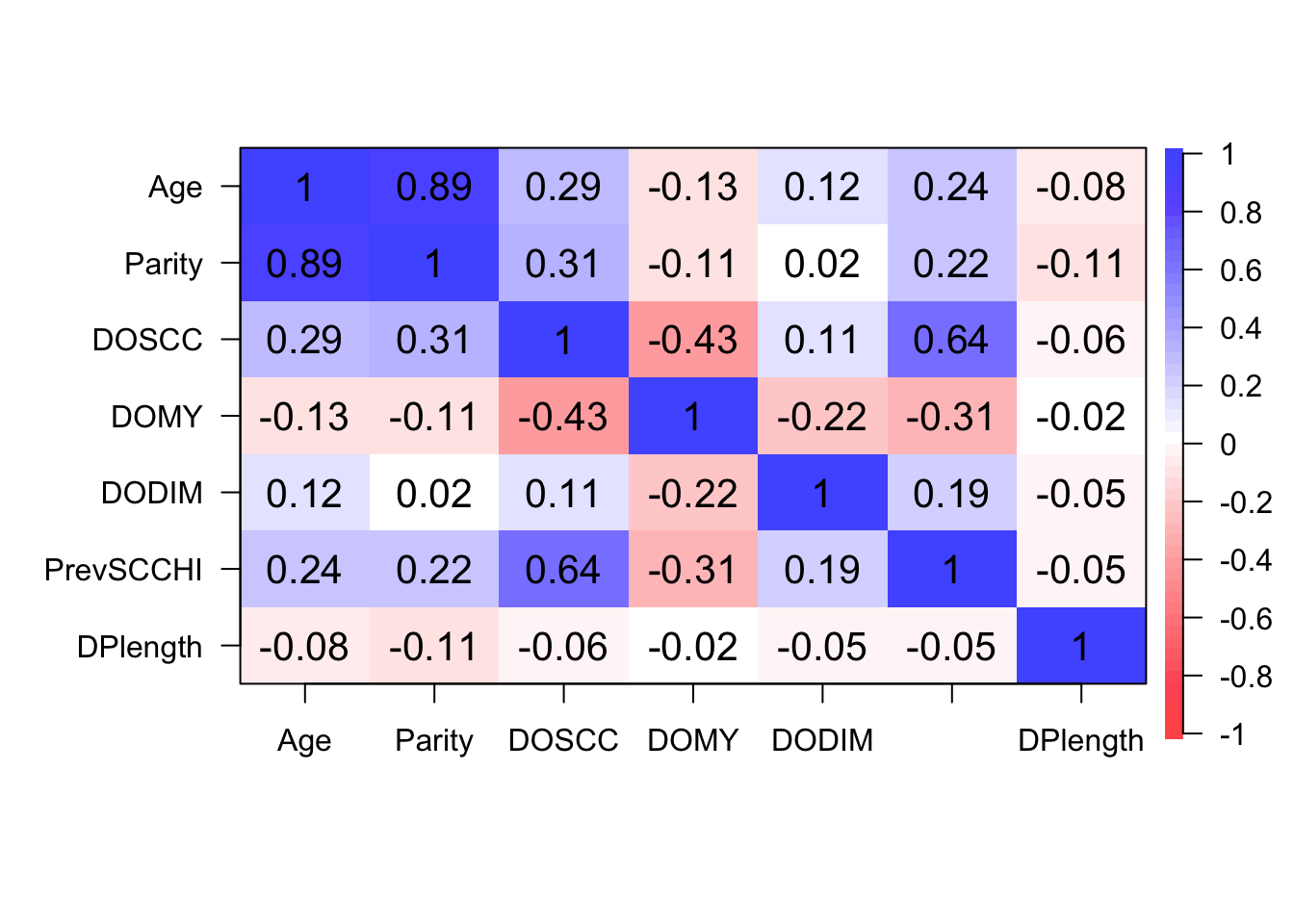
Step 2: Identify correlated variables using pearson and kendalls correlation coefficients

Step 3: Create model with all potential confounders

Step 4: Investigate if covariates meet proportional hazards assumption

Step 5: Investigate potential effect measure modification

Step 6: Remove unneccesary covariates in backwards stepwise fashion using 10% rule (i.e. if hazard ratio for algorithm or culture changes by >10% after removing the covariate, the covariate is retained in the model)

Step 7: Report final model




Step 1: DAG for clincal mastitis

This is used to identify variables that could be confounders if they are not balanced between treatment groups.

library(DiagrammeR)
mermaid("graph LR
        T(Treatment)-->U(Clinical mastitis)
        A(Age)-->T
        P(Parity)-->T
        M(Yield at dry-off)-->T
        S(SCC during prev lactation)-->T
        C(CM in prev lact)-->T
        A-->U
        P-->U
        M-->U
        S-->U
        C-->U
        C-->M
        P-->C
        P-->S
        P-->M
        A-->P
        A-->C
        A-->S
        A-->M
        M-->S
        C-->S
        style A fill:#FFFFFF, stroke-width:0px
        style T fill:#FFFFFF, stroke-width:2px
        style P fill:#FFFFFF, stroke-width:0px
        style M fill:#FFFFFF, stroke-width:0px
        style S fill:#FFFFFF, stroke-width:0px
        style C fill:#FFFFFF, stroke-width:0px
        style I fill:#FFFFFF, stroke-width:0px
        style U fill:#FFFFFF, stroke-width:2px
        ")

According to this DAG, I may need to control for the following variables.

Parity [“Parity”]

Age [“Age”]

Yield at most recent test before dry off [“DOMY”]

Somatic cell count at last herd test during previous lactation [“DOSCC” or “PrevSCCHi”] <- likely to be correlated

Clinical mastitis in previous lactation [“PrevCM”]





Step 2: Identify correlated covariates

Pearson correlation matrix among potential predictors

library(psych)
cor <- Baseline[, c(6,7,9,10,11,13,14)]
cor$Parity <- as.numeric(cor$Parity)
cor <- cor(cor, use = "complete.obs")
corPlot(cor, numbers=T)

cor <- Baseline[, c(6,7,9,10,11,13,14)]
cor$Parity <- as.numeric(cor$Parity)
cor <- cor(cor, use = "complete.obs",method="kendal")
corPlot(cor, numbers=T)

Age and Parity highly correlated as expected. Will only offer parity.

Previous lactation peak SCC is moderately correlated with SCC at last herd test (DOSCC). Will only offer DOSCC.





Step 3: Create model with all potential covariates

Cox proportional hazards regression for clinical mastitis (1-120 DIM)

Cows that did not calve or that had long/short dry periods are excluded. Cows with clinical mastitis prior to calving are included.

Reasons for R censor = 120 DIM or culling/death

SR <- coxph(Surv(CMTAR, CM) ~ Parity + DOMY + DOSCC + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
coxph(Surv(CMTAR, CM) ~ Parity + DOMY + DOSCC + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
## Call:
## coxph(formula = Surv(CMTAR, CM) ~ Parity + DOMY + DOSCC + PrevCM + 
##     Tx + cluster(FARMID), data = SDCTCOW)
## 
##                  coef exp(coef)  se(coef) robust se      z      p
## Parity2      0.262972  1.300790  0.198272  0.127747  2.059 0.0395
## Parity3      0.328493  1.388873  0.204918  0.292867  1.122 0.2620
## DOMY        -0.006115  0.993904  0.010031  0.018794 -0.325 0.7449
## DOSCC        0.028361  1.028767  0.076123  0.105980  0.268 0.7890
## PrevCM1      0.357508  1.429761  0.212265  0.228486  1.565 0.1177
## TxCulture   -0.193527  0.824048  0.192911  0.177916 -1.088 0.2767
## TxAlgorithm -0.173991  0.840304  0.194505  0.162762 -1.069 0.2851
## 
## Likelihood ratio test=10.21  on 7 df, p=0.1771
## n= 1211, number of events= 157
#tidy(coxph(Surv(CMTAR, CM) ~ Tx + cluster(FARMID), data=SDCTCOW))




Step 4: Schoenfield tests to assess assumption of proportional hazards for explanatory variables.

Parity, Tx and DOSCC violate the assumption of proportional hazards

SR <- cox.zph(SR)
SR
##                 rho  chisq        p
## Parity2     -0.1172  4.313 0.037831
## Parity3     -0.1245 11.662 0.000638
## DOMY         0.0370  1.843 0.174616
## DOSCC        0.1043  5.489 0.019134
## PrevCM1      0.0207  0.394 0.530189
## TxCulture    0.1564  9.946 0.001612
## TxAlgorithm  0.0207  0.480 0.488505
## GLOBAL           NA 14.007 0.051053





Schoenfield residual plots to assess assumption of proportional hazards.

ggcoxzph(SR,var = c("TxCulture","TxAlgorithm"))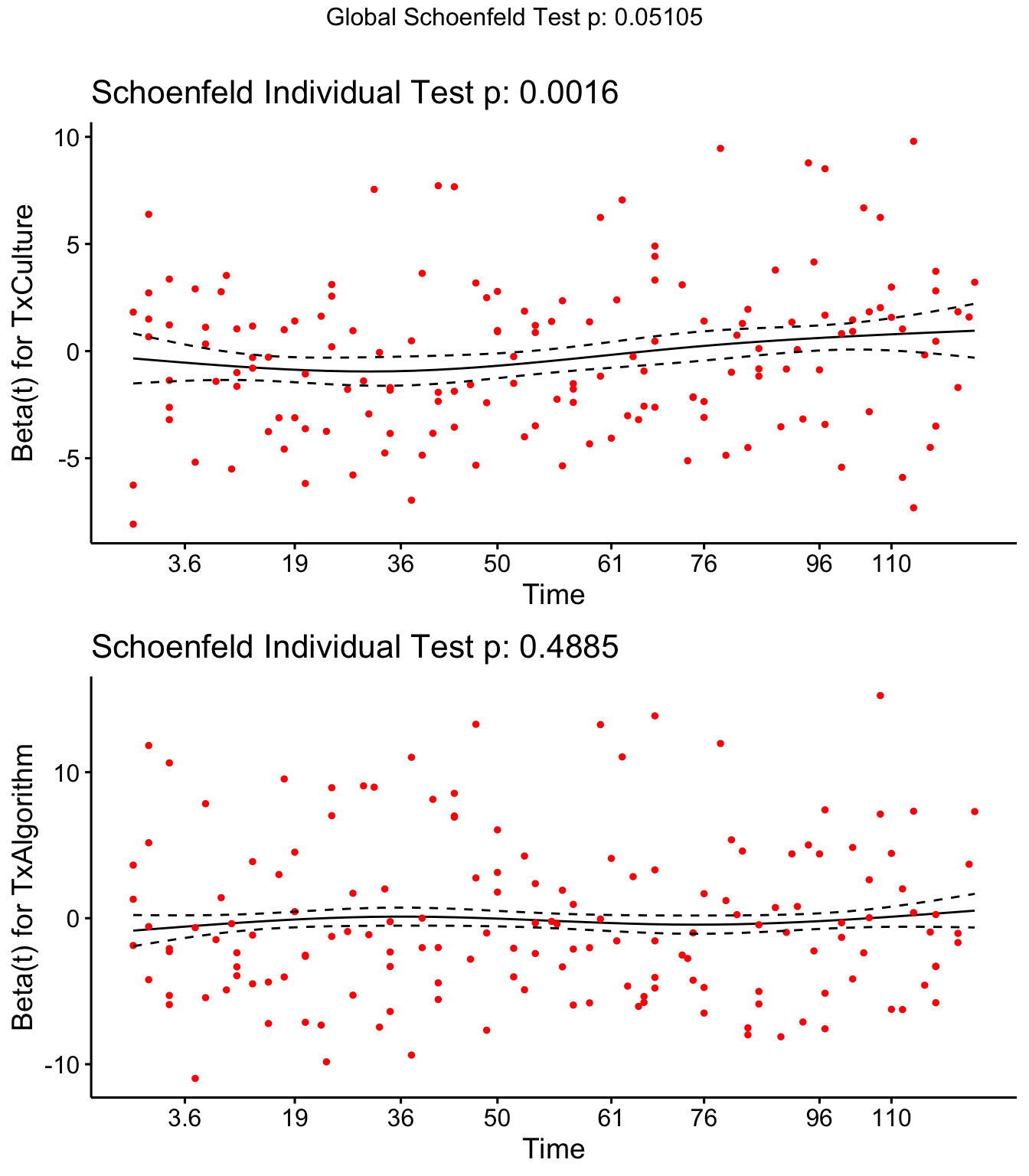

ggcoxzph(SR,var = c("DOSCC", "DOMY"))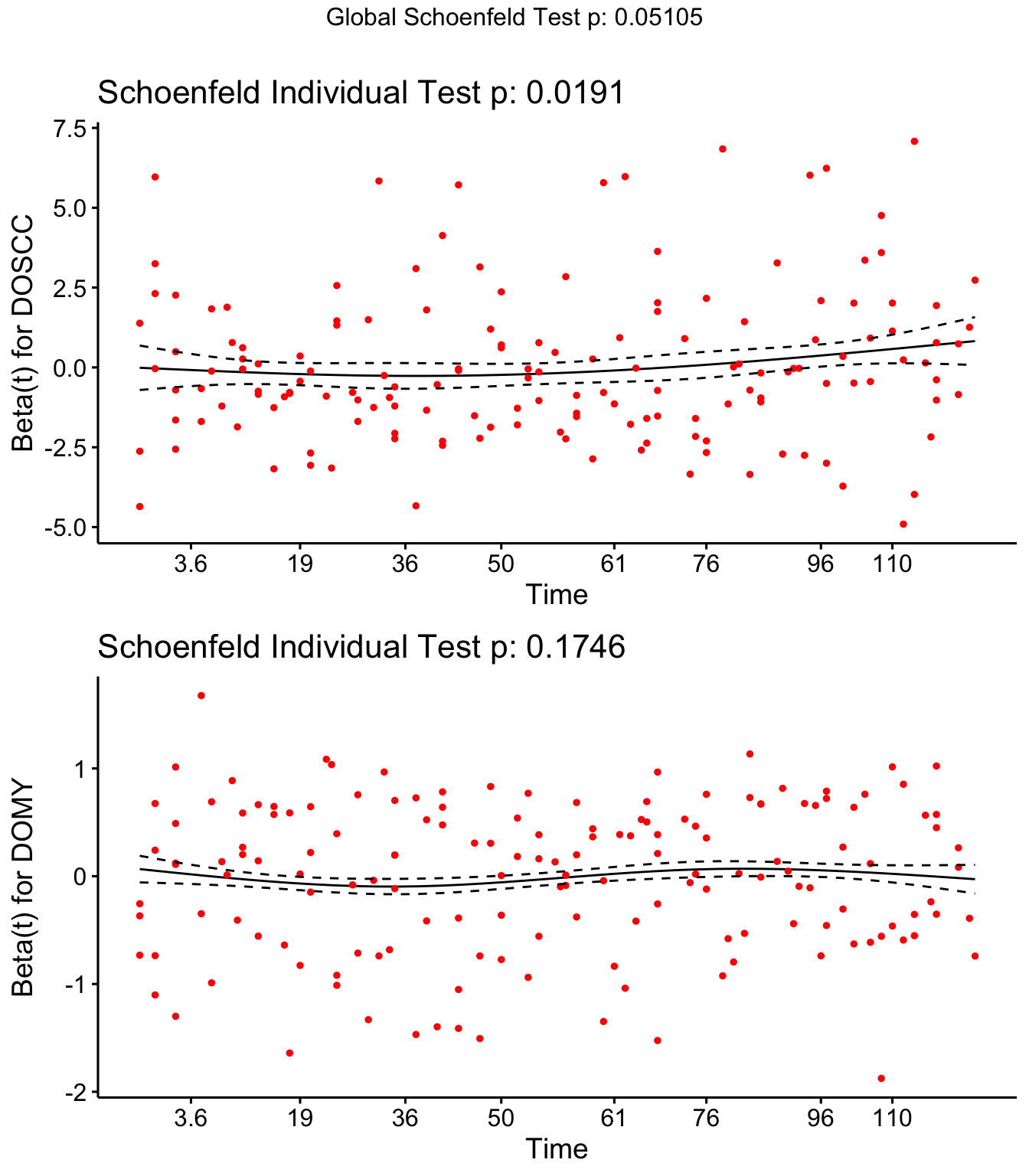

ggcoxzph(SR,var = c("Parity2","Parity3"))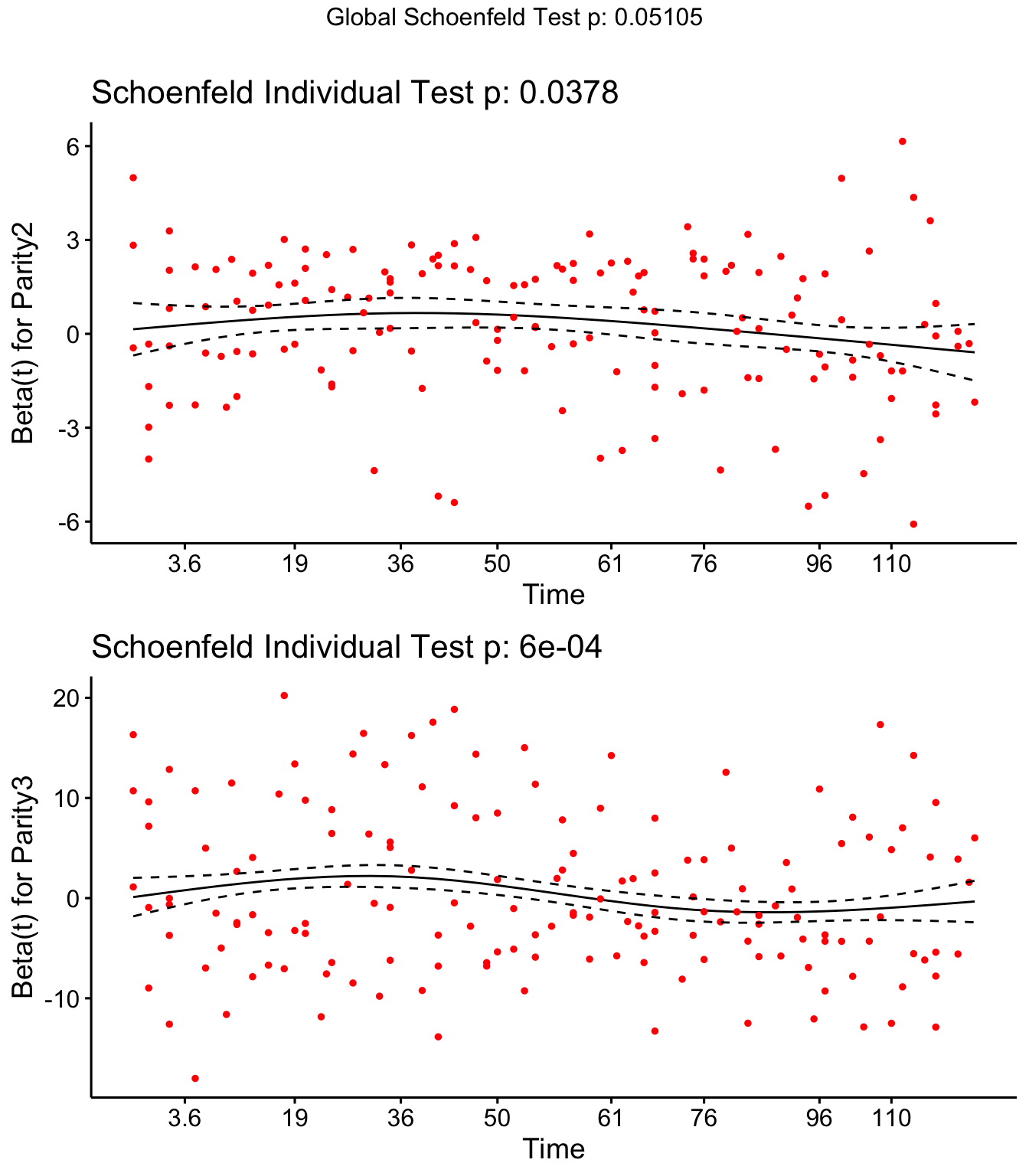

ggcoxzph(SR,var = c("PrevCM1"))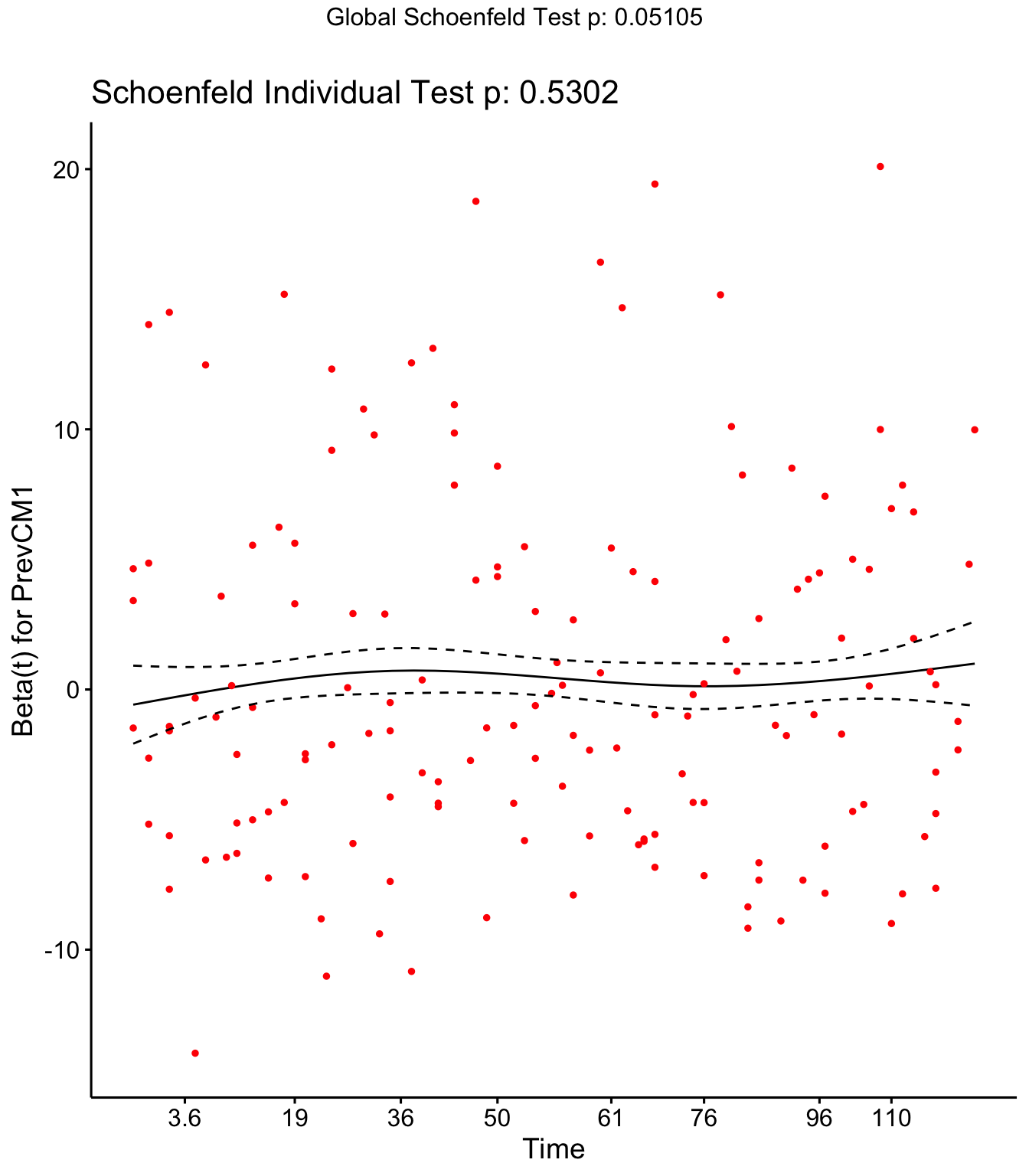





I will deal with these covariates using stratification (i.e. fitting seperate baseline hazards)

I must create categorical variables to allow for this (not shown here).

Dry off milk yield [“DOMY”] -> median split (“DOMYcat” = 0 / 1).

Dry off SCC - split at 200,000 cells (subclinical mastitis [“DOSCM”] = 0 / 1)





Show new variables

SDCTCOWcheck <- SDCTCOW %>% select(Tx,CM,CMTAR,Cull2,Cull2TAR,DOSCC,DOSCM,DOMY,DOMYcat,Parity,PrevCM)
head(SDCTCOWcheck)





Run new cox model with stratified variables

library(broom)
SR <- coxph(Surv(CMTAR, CM) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
tidy(coxph(Surv(CMTAR, CM) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW))





Repeat Schoenfeld residuals

Tx no longer p < 0.05, but is close to the threshold (p = 0.08).

SR <- cox.zph(SR)
SR
##                rho chisq      p
## PrevCM1     0.0273 0.185 0.6674
## TxCulture   0.1393 3.094 0.0786
## TxAlgorithm 0.0442 0.419 0.5173
## GLOBAL          NA 3.320 0.3449





Will split time into 1-60 and 61-120 DIM to see if this difference is meaningful.

Cox model 1-60 DIM

Beta coefficient for Culture = -0.43, Algorithm = -0.08

SR <- coxph(Surv(CMTAR60, CM60) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
tidy(coxph(Surv(CMTAR60, CM60) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW))





Cox model 61-120 DIM Beta coefficient for Culture = 0.008, Algorithm = -.401

SR <- coxph(Surv(CMTAR60120, CM60120) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
tidy(coxph(Surv(CMTAR60120, CM60120) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW))

Decision: These differences aren’t sufficient in my opinion to warrant pursuing the 1-60, 61-120 DIM models. An average of the two is appropriate.



Step 5: Investigate effect measure modification

Unable to evluate interaction between Tx & FARMID using Cox regression - Bizzare SE’s, won’t converge.

mm0 <- coxph(Surv(CMTAR, CM) ~ Tx + FARMID + Tx:FARMID + PrevCM + strata(Parity) + strata(DOMYcat) + strata(DOSCM), data=SDCTCOW)
tidy(mm0)





Will use logistic regression to assess for interaction between Tx and farm: P > 0.05.

mm0 <- glm(CM ~ Tx*FARMID + PrevCM + Parity + DOMYcat + DOSCM, data=SDCTCOW, family=binomial)
car::Anova(mm0)

Decision: No treatment by herd effect measure modification





Assess effect measure modification with previous clinical mastitis using Cox regression.

a <- coxph(Surv(CMTAR, CM) ~ factor(Tx)*factor(PrevCM) + strata(Parity) + cluster(FARMID) + strata(DOMYcat) + strata(DOSCM), data=SDCTCOW)

library(aod)
wald.test(b = coef(a), Sigma = vcov(a), Terms = 4:5)
## Wald test:
## ----------
## 
## Chi-squared test:
## X2 = 11.0, df = 2, P(> X2) = 0.004

Wald test for interaction is p < 0.05.



Model output with interaction

mm0 <- coxph(Surv(CMTAR, CM) ~ Tx*PrevCM + strata(Parity) + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW)
tidy(mm0)

According to this interaction model, the HR (referent = Blanket Tx, no prev CM) for each group are:

Blanket:Prev0 = 1

Blanket:Prev1 = 2.1

Culture:PrevCM0 = 0.93

Culture:PrevCM1 = 0.97

Algorithm:PrevCM0 = 0.93

Algorithm:PrevCM1 = 1.14

This is a counter-intuitive result: hazards of clinical mastitis are higher in blanket cows with previous history of CM.

However, these effect estimates have wide confidence intervals, and this interaction model adds unnecessary complexity and does not change our conclusions.

Decision: Report main effects.





Step 6: Remove unnecessary covariates (backwards selection using 10% rule)

The order for removing covariates will be in increasing likelihood of being a confounder, which is based on my knowledge about the variables and their distribution in treatment groups.

This order will be: DOMYcat, DOSCM, Parity, PrevCM

Step 6a: Full model

mm0 <- tidy(coxph(Surv(CMTAR, CM) ~ strata(Parity) + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)) %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0





Step 6b: removing DOMYcat

mm0 <- tidy(coxph(Surv(CMTAR, CM) ~ strata(Parity) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW))%>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

Both HR (Culture and Algorithm) changed by <10%. DOMYcat stays out.



Step 6c: removing DOSCM

mm0 <- tidy(coxph(Surv(CMTAR, CM) ~ strata(Parity) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)) %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

Both HR changed by <10%. DOMYcat stays out.



Step 6d: removing Parity

mm0 <- tidy(coxph(Surv(CMTAR, CM) ~ PrevCM + Tx + cluster(FARMID), data=SDCTCOW)) %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

Both HR changed by <10%. Parity stays out.





Step 6e: removing PrevCM

mm0 <- tidy(coxph(Surv(CMTAR, CM) ~ Tx + cluster(FARMID), data=SDCTCOW)) %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

Both HR changed by <10%. PrevCM stays out.



Step 7a: Reporting final cox model for clinical mastitis (1-120 DIM)

No covariates included, as no evidence for confounding.

CoxCM <- tidy(coxph(Surv(CMTAR, CM) ~ Tx + cluster(FARMID), data=SDCTCOW))
CoxCM$HR <- exp(CoxCM$estimate)
CoxCM$LCL <- exp(CoxCM$conf.low)
CoxCM$UCL <- exp(CoxCM$conf.high)
CoxCM <- CoxCM %>% select(term,HR,LCL,UCL,robust.se,p.value)
CoxCM




Checking Schoenfield residuals for Tx in final model

SR <- coxph(Surv(CMTAR, CM) ~ Tx + cluster(FARMID), data=SDCTCOW)
cox.zph(SR)
##                  rho    chisq     p
## TxCulture    0.12471 2.077891 0.149
## TxAlgorithm -0.00225 0.000429 0.983
## GLOBAL            NA 2.596282 0.273
SR <- cox.zph(SR)
ggcoxzph(SR,var = c("TxCulture","TxAlgorithm"))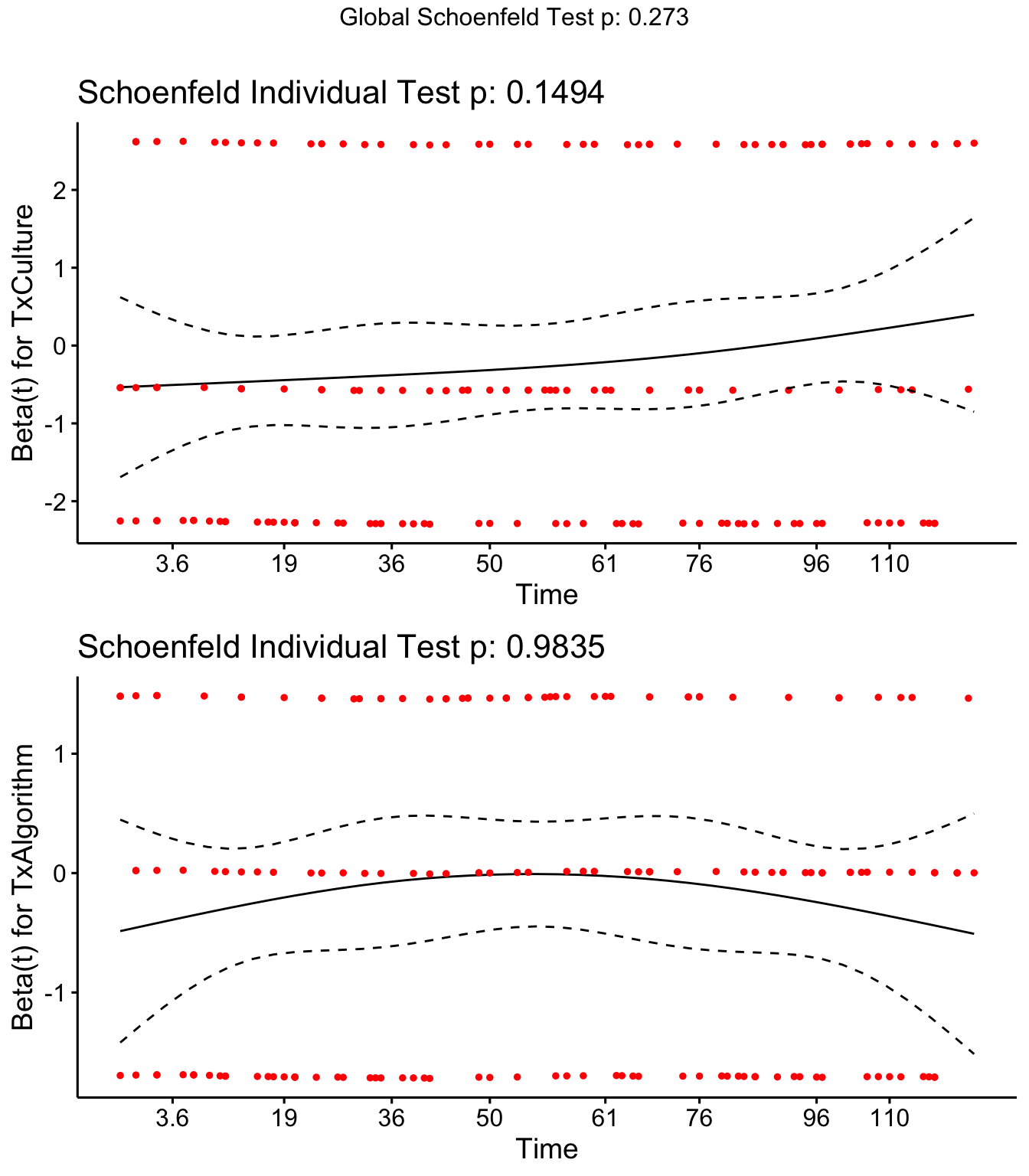

Sufficient evidence to use Cox model.




Step 7b: Reporting final cox model for clinical mastitis (1-120 DIM) using P-value based backwards stepwise selection

CoxCM <- coxph(Surv(CMTAR, CM) ~ Tx + Parity + cluster(FARMID), data=SDCTCOW) %>% tidy()
CoxCM$HR <- exp(CoxCM$estimate)
CoxCM$LCL <- exp(CoxCM$conf.low)
CoxCM$UCL <- exp(CoxCM$conf.high)
CoxCM <- CoxCM %>% select(term,HR,LCL,UCL,robust.se,p.value)
CoxCM

Estimates are very similar to those found using 10% rule.



Outcome 2: Culling / Death

Kaplan Meier curve & log rank test for culling/death

library(gmodels)
CrossTable(SDCTCOW$Tx,SDCTCOW$Cull2,prop.c=FALSE,prop.t=FALSE,prop.chisq = FALSE)
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  1211 
## 
##  
##              | SDCTCOW$Cull2 
##   SDCTCOW$Tx |         0 |         1 | Row Total | 
## -------------|-----------|-----------|-----------|
##      Blanket |       363 |        44 |       407 | 
##              |     0.892 |     0.108 |     0.336 | 
## -------------|-----------|-----------|-----------|
##      Culture |       370 |        40 |       410 | 
##              |     0.902 |     0.098 |     0.339 | 
## -------------|-----------|-----------|-----------|
##    Algorithm |       352 |        42 |       394 | 
##              |     0.893 |     0.107 |     0.325 | 
## -------------|-----------|-----------|-----------|
## Column Total |      1085 |       126 |      1211 | 
## -------------|-----------|-----------|-----------|
## 
##

Kaplan Meier curve

KM <- survfit(Surv(Cull2TAR, Cull2) ~ Tx, data = SDCTCOW)
ggsurvplot(KM, data = SDCTCOW,  title = "", pval = T, conf.int = F,risk.table.col = "Tx",risk.table = T, risk.table.y.text.col = TRUE , surv.plot.height = 5, legend.labs = c("Blanket","Culture","Algorithm"), tables.theme = theme_cleantable(), ggtheme = theme_bw())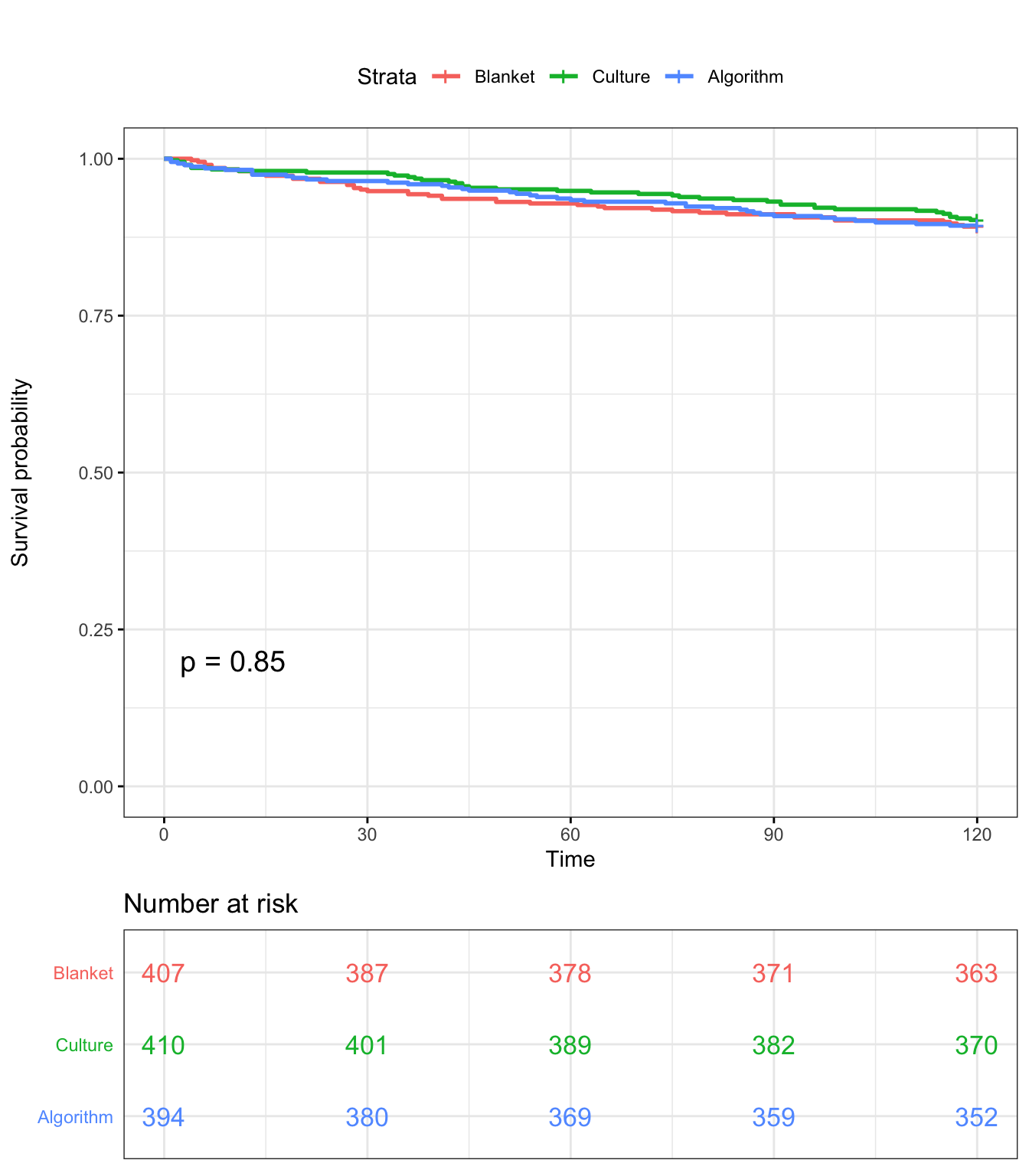





Log-Rank test

survdiff(Surv(Cull2TAR, Cull2) ~ Tx,data=SDCTCOW,rho=0)
## Call:
## survdiff(formula = Surv(Cull2TAR, Cull2) ~ Tx, data = SDCTCOW, 
##     rho = 0)
## 
##                N Observed Expected (O-E)^2/E (O-E)^2/V
## Tx=Blanket   407       44     42.1    0.0891     0.134
## Tx=Culture   410       40     43.0    0.2128     0.323
## Tx=Algorithm 394       42     40.9    0.0290     0.043
## 
##  Chisq= 0.3  on 2 degrees of freedom, p= 0.8




Cox proportional hazards regression for culling or death (1-120 DIM)

Model building plan

Model type: Cox proportional hazards analysis with farm included as a cluster variable to account for lack of indepedence.

Step 1: Identify potential confouders using a directed acyclic graph (DAG)

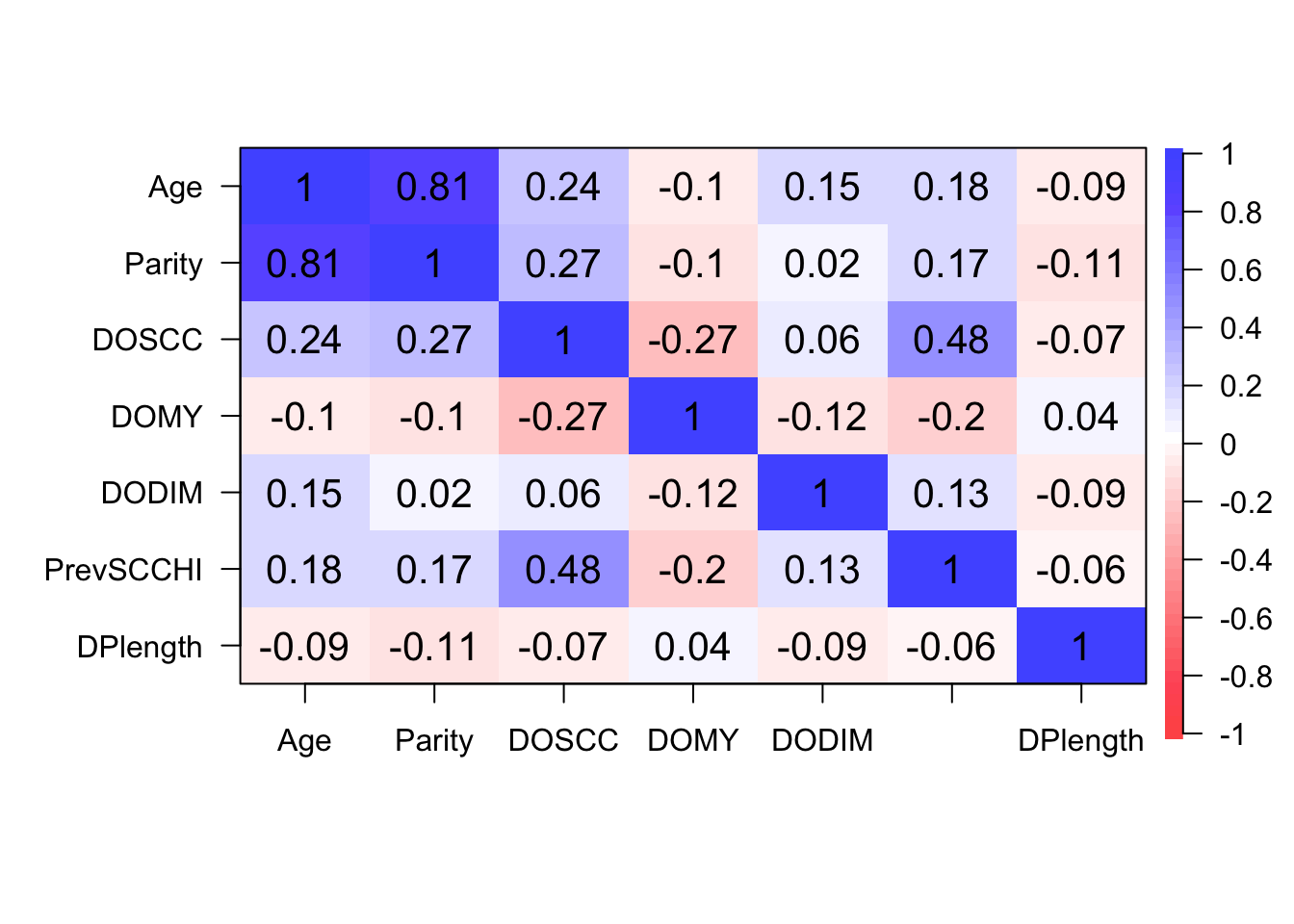
Step 2: Identify correlated variables using pearson and kendalls correlation coefficients

Step 3: Create model with all potential confounders

Step 4: Investigate if covariates meet proportional hazards assumption

Step 5: Investigate potential effect measure modification

Step 6: Remove unneccesary covariates in backwards stepwise fashion using 10% rule (i.e. if HR changes by >10% after removal of covariate, the covariate is retained in the model)

Step 7: Report final model

Steps 1 & 2: Identify potential confouders using a directed acyclic graph (DAG)

library(DiagrammeR)
mermaid("graph LR
        T(Treatment)-->U(Culling or Death)
        A(Age)-->T
        P(Parity)-->T
        M(Yield at dry-off)-->T
        S(SCC during prev lactation)-->T
        C(CM in prev lact)-->T
        A-->U
        P-->U
        M-->U
        S-->U
        C-->U
        C-->M
        P-->C
        P-->S
        P-->M
        A-->P
        A-->C
        A-->S
        A-->M
        M-->S
        C-->S
        style A fill:#FFFFFF, stroke-width:0px
        style T fill:#FFFFFF, stroke-width:2px
        style P fill:#FFFFFF, stroke-width:0px
        style M fill:#FFFFFF, stroke-width:0px
        style S fill:#FFFFFF, stroke-width:0px
        style C fill:#FFFFFF, stroke-width:0px
        style I fill:#FFFFFF, stroke-width:0px
        style U fill:#FFFFFF, stroke-width:2px
        ")

According to this DAG, I may need to control for the following variables:

Parity [“Parity”]. Will not offer Age [“Age”] as it is highly correlated.

Yield at most recent test before dry off [“DOMY”]

Somatic cell count at last herd test during previous lactation [“DOSCC”] <- will not offer PrevSCCHI as it was correlated with DOSCC

Clinical mastitis in previous lactation [“PrevCM”]





Step 3: Create model with all potential confounders

Cows that did not calve are excluded (left censored)

Reason for R censor = 120 DIM

library(broom)
library(survival)
coxph(Surv(Cull2TAR, Cull2) ~ Parity + DOMY + DOSCC + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
## Call:
## coxph(formula = Surv(Cull2TAR, Cull2) ~ Parity + DOMY + DOSCC + 
##     PrevCM + Tx + cluster(FARMID), data = SDCTCOW)
## 
##                 coef exp(coef) se(coef) robust se      z        p
## Parity2      0.39524   1.48475  0.25866   0.21257  1.859  0.06298
## Parity3      1.13923   3.12436  0.23351   0.23115  4.929 8.29e-07
## DOMY        -0.01446   0.98564  0.01107   0.01471 -0.983  0.32560
## DOSCC        0.08981   1.09396  0.08514   0.05241  1.714  0.08660
## PrevCM1      0.26788   1.30719  0.22819   0.09322  2.874  0.00406
## TxCulture   -0.09850   0.90619  0.21940   0.21233 -0.464  0.64271
## TxAlgorithm  0.01074   1.01079  0.21583   0.23312  0.046  0.96327
## 
## Likelihood ratio test=44.51  on 7 df, p=1.706e-07
## n= 1211, number of events= 126





Step 4: Investigate if covariates meet proportional hazards assumption

Both DOSCC and DOMY don’t meet the assumption of proportional hazards

SR <- cox.zph(coxph(Surv(Cull2TAR, Cull2) ~ Parity + DOMY + DOSCC + PrevCM + Tx + cluster(FARMID), data=SDCTCOW))
SR
##                 rho chisq       p
## Parity2     -0.1157 2.607 0.10639
## Parity3     -0.0343 0.209 0.64753
## DOMY         0.1521 7.402 0.00652
## DOSCC        0.1462 5.471 0.01934
## PrevCM1     -0.1220 2.530 0.11172
## TxCulture    0.1222 3.313 0.06872
## TxAlgorithm  0.0815 1.396 0.23741
## GLOBAL           NA 8.182 0.31686




Schoenfield residual plots

ggcoxzph(SR,var = c("TxCulture","TxAlgorithm"))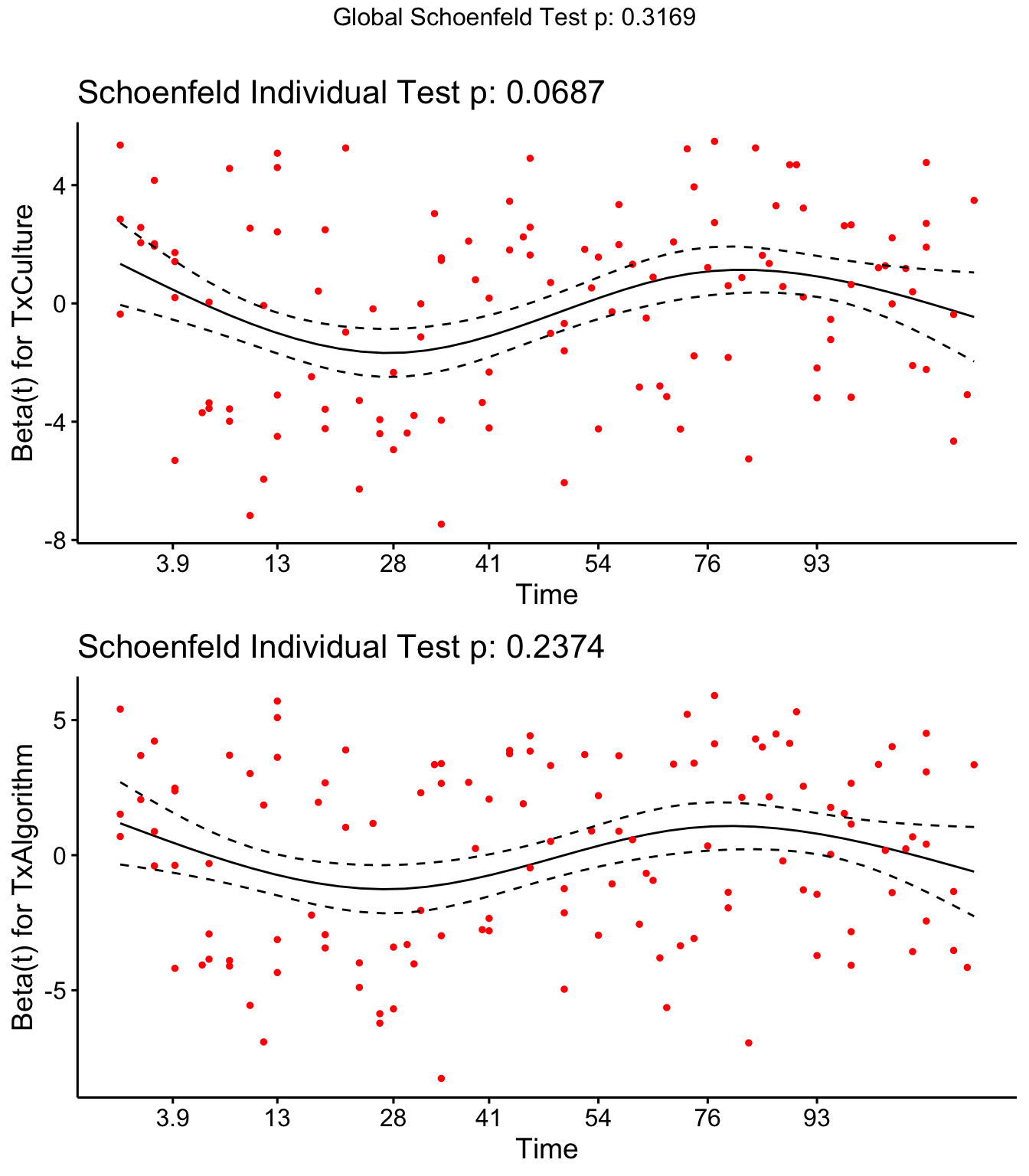





DOSCC and DOMY don’t meet the assumption of proportional hazards

ggcoxzph(SR,var = c("DOSCC", "DOMY"))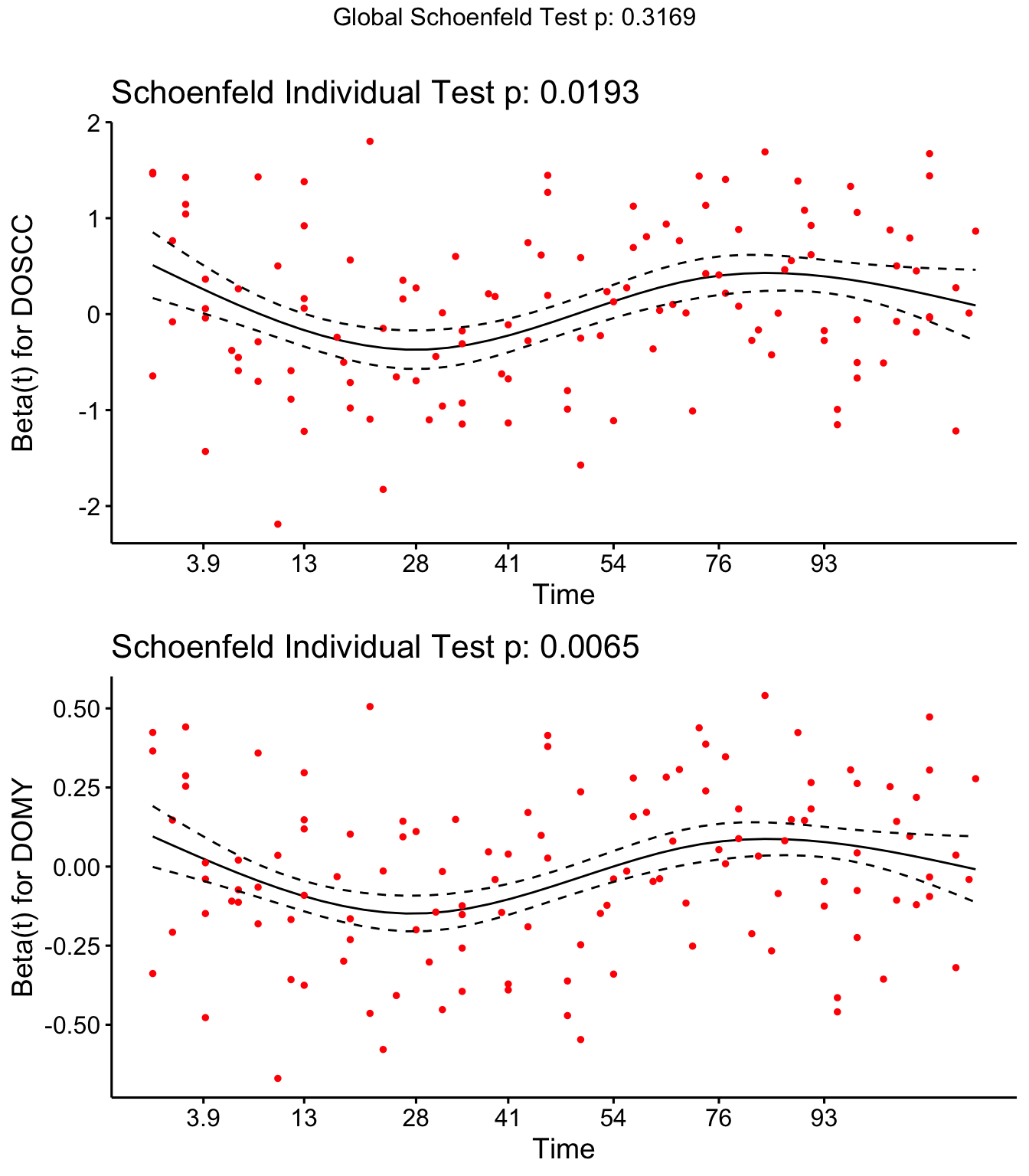

ggcoxzph(SR,var = c("Parity2","Parity3"))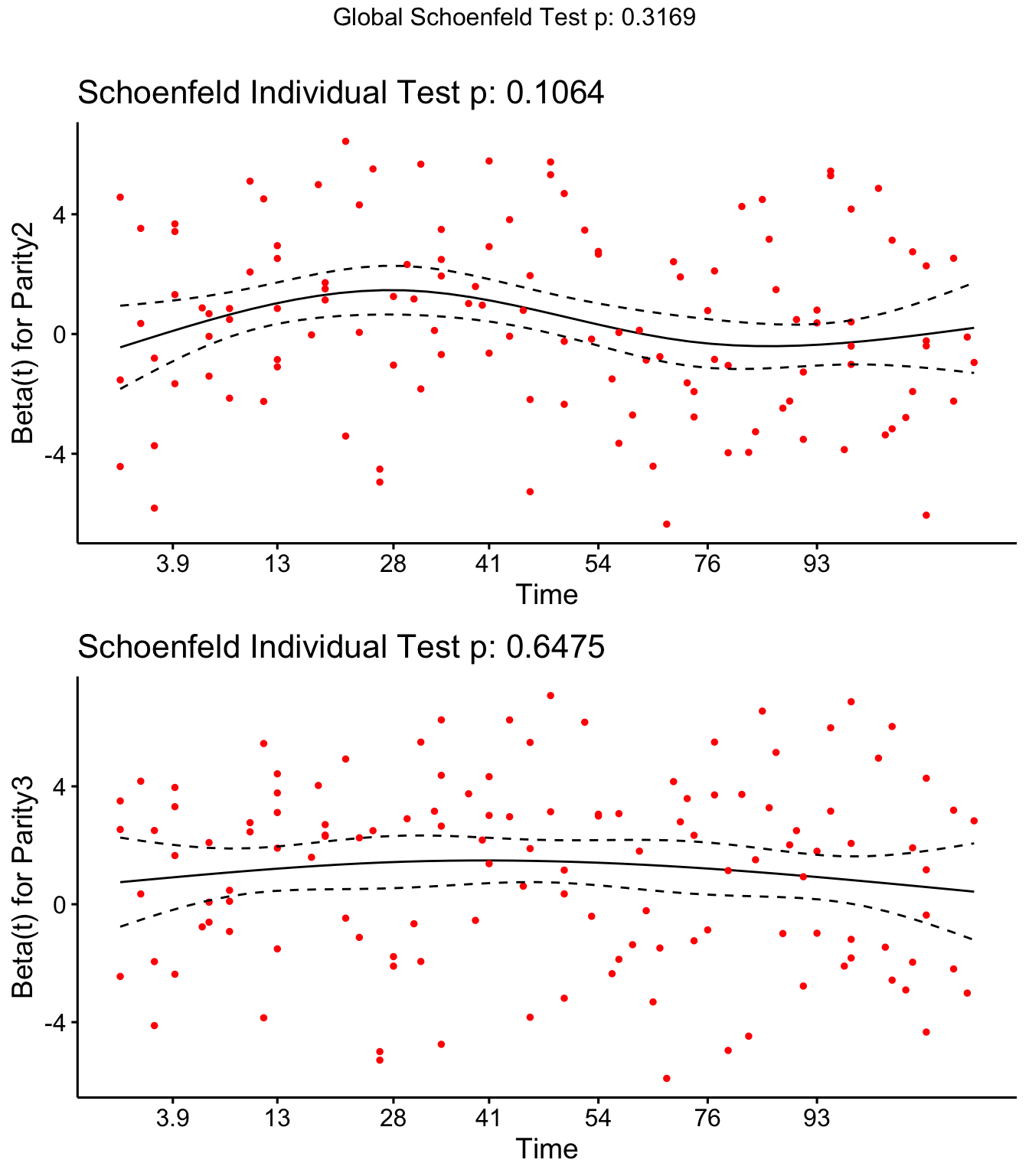

ggcoxzph(SR,var = c("PrevCM1"))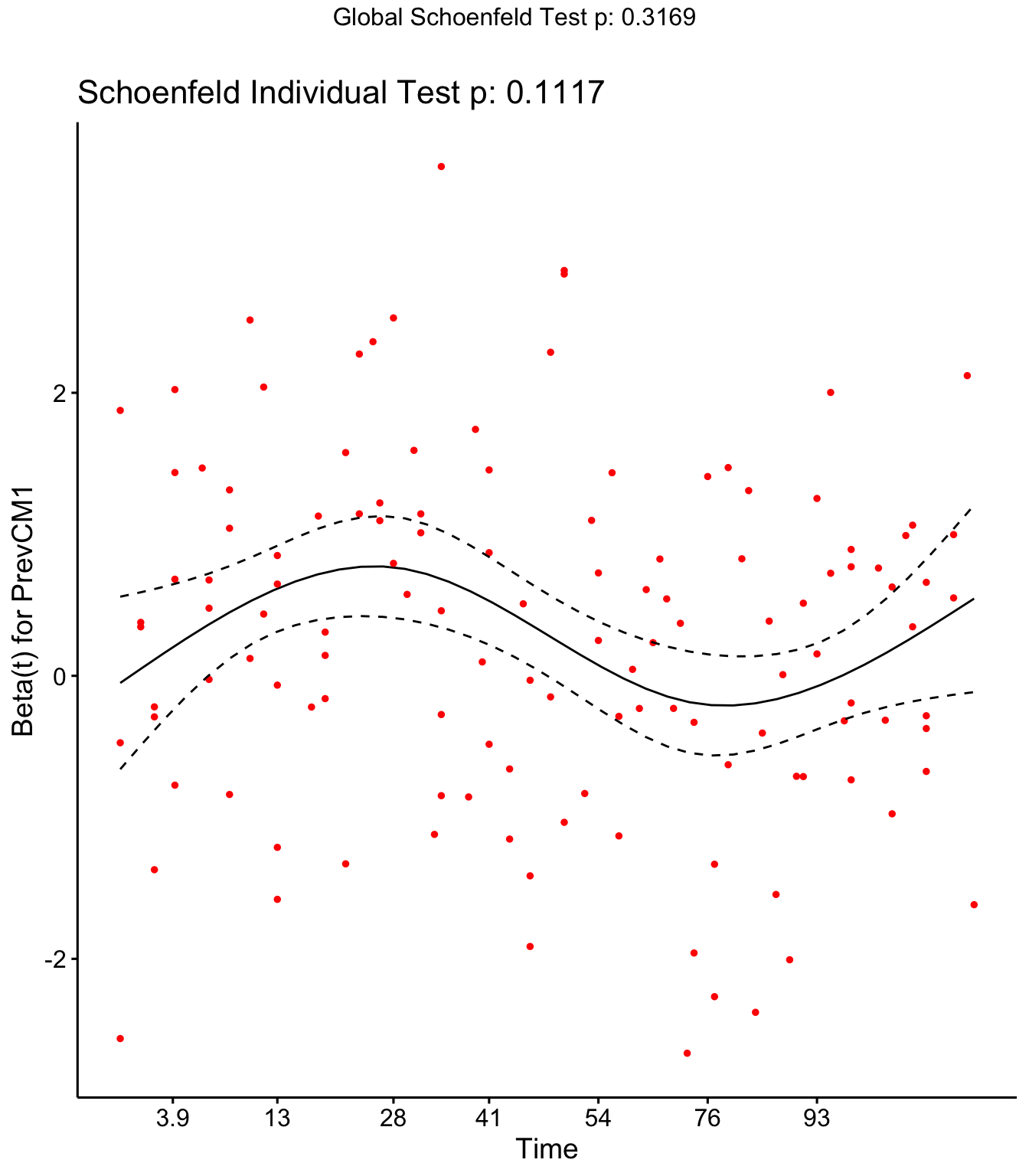





Refit cox model with seperate baselines (stratified) for DOMY and DOSCC.

No evidence of other time-varying covariates or predictors (Tx).

SR <- coxph(Surv(Cull2TAR, Cull2) ~ Parity + strata(DOMYcat) + strata(DOSCM) + PrevCM + Tx + cluster(FARMID), data=SDCTCOW)
SR <- cox.zph(SR)
SR
##                  rho    chisq     p
## Parity2     -0.05884 0.412749 0.521
## Parity3     -0.00113 0.000217 0.988
## PrevCM1     -0.06962 0.500950 0.479
## TxCulture    0.10086 1.689182 0.194
## TxAlgorithm  0.07741 1.091294 0.296
## GLOBAL            NA 2.214228 0.819





Step 5: Assess for effect measure modification

Tx : FARMID - could not assess this using Cox regression as model did not converge or reported unusually large SEs for some interaction terms.

SR <- coxph(Surv(Cull2TAR, Cull2) ~ Tx*FARMID + Parity + PrevCM + Parity + strata(DOMYcat) + strata(DOSCM), data=SDCTCOW)
tidy(SR)





I will assess effect Tx:farm interaction using logistic regression:

Wald test for interaction term was P > 0.05.

mm0 <- glm(CM ~ Tx*FARMID + Parity + PrevCM + Parity + DOMYcat + DOSCM, data=SDCTCOW)
car::Anova(mm0)





Assess for other interactions using Wald testfrom Cox regression.

Wald test was P > 0.05 for Tx:PrevCM interaction

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx*PrevCM + Parity + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW)
summary(mm0)
## Call:
## coxph(formula = Surv(Cull2TAR, Cull2) ~ Tx * PrevCM + Parity + 
##     strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data = SDCTCOW)
## 
##   n= 1211, number of events= 126 
## 
##                         coef exp(coef) se(coef) robust se      z Pr(>|z|)
## TxCulture           -0.02411   0.97618  0.24667   0.23595 -0.102   0.9186
## TxAlgorithm          0.05495   1.05649  0.24266   0.27674  0.199   0.8426
## PrevCM1              0.49435   1.63943  0.36416   0.20400  2.423   0.0154
## Parity2              0.41575   1.51550  0.25731   0.21398  1.943   0.0520
## Parity3              1.17829   3.24881  0.23075   0.25675  4.589 4.45e-06
## TxCulture:PrevCM1   -0.40970   0.66385  0.53890   0.33877 -1.209   0.2265
## TxAlgorithm:PrevCM1 -0.21937   0.80303  0.53502   0.70719 -0.310   0.7564
##                        
## TxCulture              
## TxAlgorithm            
## PrevCM1             *  
## Parity2             .  
## Parity3             ***
## TxCulture:PrevCM1      
## TxAlgorithm:PrevCM1    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                     exp(coef) exp(-coef) lower .95 upper .95
## TxCulture              0.9762     1.0244    0.6147     1.550
## TxAlgorithm            1.0565     0.9465    0.6142     1.817
## PrevCM1                1.6394     0.6100    1.0991     2.445
## Parity2                1.5155     0.6598    0.9964     2.305
## Parity3                3.2488     0.3078    1.9642     5.374
## TxCulture:PrevCM1      0.6638     1.5064    0.3417     1.290
## TxAlgorithm:PrevCM1    0.8030     1.2453    0.2008     3.211
## 
## Concordance= 0.64  (se = 0.03 )
## Likelihood ratio test= 33.79  on 7 df,   p=2e-05
## Wald test            = 1281  on 7 df,   p=<2e-16
## Score (logrank) test = 36.55  on 7 df,   p=6e-06,   Robust = 7  p=0.4
## 
##   (Note: the likelihood ratio and score tests assume independence of
##      observations within a cluster, the Wald and robust score tests do not).
wald.test(b = coef(mm0), Sigma = vcov(mm0), Terms = 6:7)
## Wald test:
## ----------
## 
## Chi-squared test:
## X2 = 1.6, df = 2, P(> X2) = 0.46





Wald test was P < 0.05 for Tx:Parity interaction .

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx*Parity + PrevCM + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW)
summary(mm0)
## Call:
## coxph(formula = Surv(Cull2TAR, Cull2) ~ Tx * Parity + PrevCM + 
##     strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data = SDCTCOW)
## 
##   n= 1211, number of events= 126 
## 
##                        coef exp(coef) se(coef) robust se      z Pr(>|z|)
## TxCulture            0.5382    1.7130   0.5005    0.4124  1.305 0.191869
## TxAlgorithm          0.5758    1.7786   0.5080    0.5537  1.040 0.298327
## Parity2              0.8960    2.4498   0.4961    0.4546  1.971 0.048749
## Parity3              1.7523    5.7680   0.4572    0.4022  4.357 1.32e-05
## PrevCM1              0.3018    1.3522   0.2277    0.1047  2.882 0.003946
## TxCulture:Parity2   -0.6590    0.5173   0.6640    0.7136 -0.924 0.355691
## TxAlgorithm:Parity2 -0.6252    0.5352   0.6531    0.6359 -0.983 0.325518
## TxCulture:Parity3   -0.8959    0.4082   0.5861    0.2552 -3.511 0.000446
## TxAlgorithm:Parity3 -0.7392    0.4775   0.5900    0.4252 -1.739 0.082111
##                        
## TxCulture              
## TxAlgorithm            
## Parity2             *  
## Parity3             ***
## PrevCM1             ** 
## TxCulture:Parity2      
## TxAlgorithm:Parity2    
## TxCulture:Parity3   ***
## TxAlgorithm:Parity3 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                     exp(coef) exp(-coef) lower .95 upper .95
## TxCulture              1.7130     0.5838    0.7633    3.8440
## TxAlgorithm            1.7786     0.5622    0.6009    5.2648
## Parity2                2.4498     0.4082    1.0049    5.9721
## Parity3                5.7680     0.1734    2.6224   12.6871
## PrevCM1                1.3522     0.7395    1.1014    1.6602
## TxCulture:Parity2      0.5173     1.9329    0.1278    2.0949
## TxAlgorithm:Parity2    0.5352     1.8686    0.1539    1.8610
## TxCulture:Parity3      0.4082     2.4496    0.2476    0.6731
## TxAlgorithm:Parity3    0.4775     2.0943    0.2075    1.0987
## 
## Concordance= 0.651  (se = 0.025 )
## Likelihood ratio test= 35.95  on 9 df,   p=4e-05
## Wald test            = 89593  on 9 df,   p=<2e-16
## Score (logrank) test = 38.57  on 9 df,   p=1e-05,   Robust = 7  p=0.6
## 
##   (Note: the likelihood ratio and score tests assume independence of
##      observations within a cluster, the Wald and robust score tests do not).
wald.test(b = coef(mm0), Sigma = vcov(mm0), Terms = 6:9)
## Wald test:
## ----------
## 
## Chi-squared test:
## X2 = 658.3, df = 4, P(> X2) = 0.0




Investigate potential effect measure modification by doing stratified models

Parity = 1 Frequency table

table(SDCTCOW$Tx[SDCTCOW$Parity==1],SDCTCOW$Cull2[SDCTCOW$Parity==1])
##            
##               0   1
##   Blanket   152   6
##   Culture   173  12
##   Algorithm 156  11




Model (Parity = 1)

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + PrevCM + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW[SDCTCOW$Parity==1,]) %>% tidy()
mm0$HR <- exp(mm0$estimate)
mm0$LCL <- exp(mm0$conf.low)
mm0$UCL <- exp(mm0$conf.high)
mm0 %>% select("term","HR","LCL","UCL")




Parity = 2

Frequency table

table(SDCTCOW$Tx[SDCTCOW$Parity==2],SDCTCOW$Cull2[SDCTCOW$Parity==2])
##            
##               0   1
##   Blanket   120  13
##   Culture    99   9
##   Algorithm 112  11
mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + PrevCM + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW[SDCTCOW$Parity==2,]) %>% tidy()
mm0$HR <- exp(mm0$estimate)
mm0$LCL <- exp(mm0$conf.low)
mm0$UCL <- exp(mm0$conf.high)
mm0 %>% select("term","HR","LCL","UCL")




Parity = 3 or greater

Frequency table

table(SDCTCOW$Tx[SDCTCOW$Parity==3],SDCTCOW$Cull2[SDCTCOW$Parity==3])
##            
##              0  1
##   Blanket   91 25
##   Culture   98 19
##   Algorithm 84 20
mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + PrevCM + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW[SDCTCOW$Parity==3,]) %>% tidy
mm0$HR <- exp(mm0$estimate)
mm0$LCL <- exp(mm0$conf.low)
mm0$UCL <- exp(mm0$conf.high)
mm0 %>% select("term","HR","LCL","UCL")

This finding suggests that potential culling risks associated with SDCT may be higher in parity 1 cows than in multiparous animals. However these HR estimates in all 3 parity groups are imprecise (wide confidence intervals) because of a small number of culling/death events. For example, in lactation 1 animals: 6 in BDCT, 11 in Algorithm and 12 in Culture. Therefore, this difference in effects across levels of parity may be due to chance alone, and not worth investigating too closely.

Decision: Report main effects.




Step 6: Remove unnecessary covariates (backwards selection using 10% rule)

The order for removing covariates will be in increasing likelihood of being a confounder, which is based on my knowledge about the variables and their distribution in treatment groups.

This order will be: DOMYcat, DOSCM, PrevCM, Parity

Step 6a: Full model

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + PrevCM + Parity + strata(DOMYcat) + strata(DOSCM) + cluster(FARMID), data=SDCTCOW) %>% tidy() %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0





Step 6b: removing DOMYcat

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + PrevCM + Parity + strata(DOSCM) + cluster(FARMID), data=SDCTCOW) %>% tidy() %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

HR for culture and algorithm didn’t change by >10%. DOMYcat stays out.



Step 6c: removing DOSCM

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + PrevCM + Parity + cluster(FARMID), data=SDCTCOW) %>% tidy() %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

HR changed by <10%. DOSCM stays out.



Step 6d: removing PrevCM

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + Parity + cluster(FARMID), data=SDCTCOW) %>% tidy() %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

HR changed by <10%. Leave PrevCM out.



Step 6e: removing Parity

mm0 <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + cluster(FARMID), data=SDCTCOW) %>% tidy() %>% select("term","estimate")
mm0$HR <- exp(mm0$estimate)
mm0

HR changed by <10%. Parity stays out.





Step 7a: Final cox model for culling or death (1 - 120 DIM)

No covariates included, as no evidence for confounding.

CoxCull <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + cluster(FARMID), data=SDCTCOW) %>% tidy()
CoxCull$HR <- exp(CoxCull$estimate)
CoxCull$LCL <- exp(CoxCull$conf.low)
CoxCull$UCL <- exp(CoxCull$conf.high)
CoxCull <- CoxCull %>% select(term,HR,LCL,UCL,robust.se,p.value)
CoxCull




Check schoenfield residuals for final model

SR <- coxph(Surv(Cull2TAR, Cull2) ~ Tx + cluster(FARMID), data=SDCTCOW)
cox.zph(SR)
##                rho chisq     p
## TxCulture   0.1100  1.52 0.217
## TxAlgorithm 0.0951  1.12 0.290
## GLOBAL          NA  1.53 0.466
SR <- cox.zph(SR)
ggcoxzph(SR,var = c("TxCulture","TxAlgorithm"))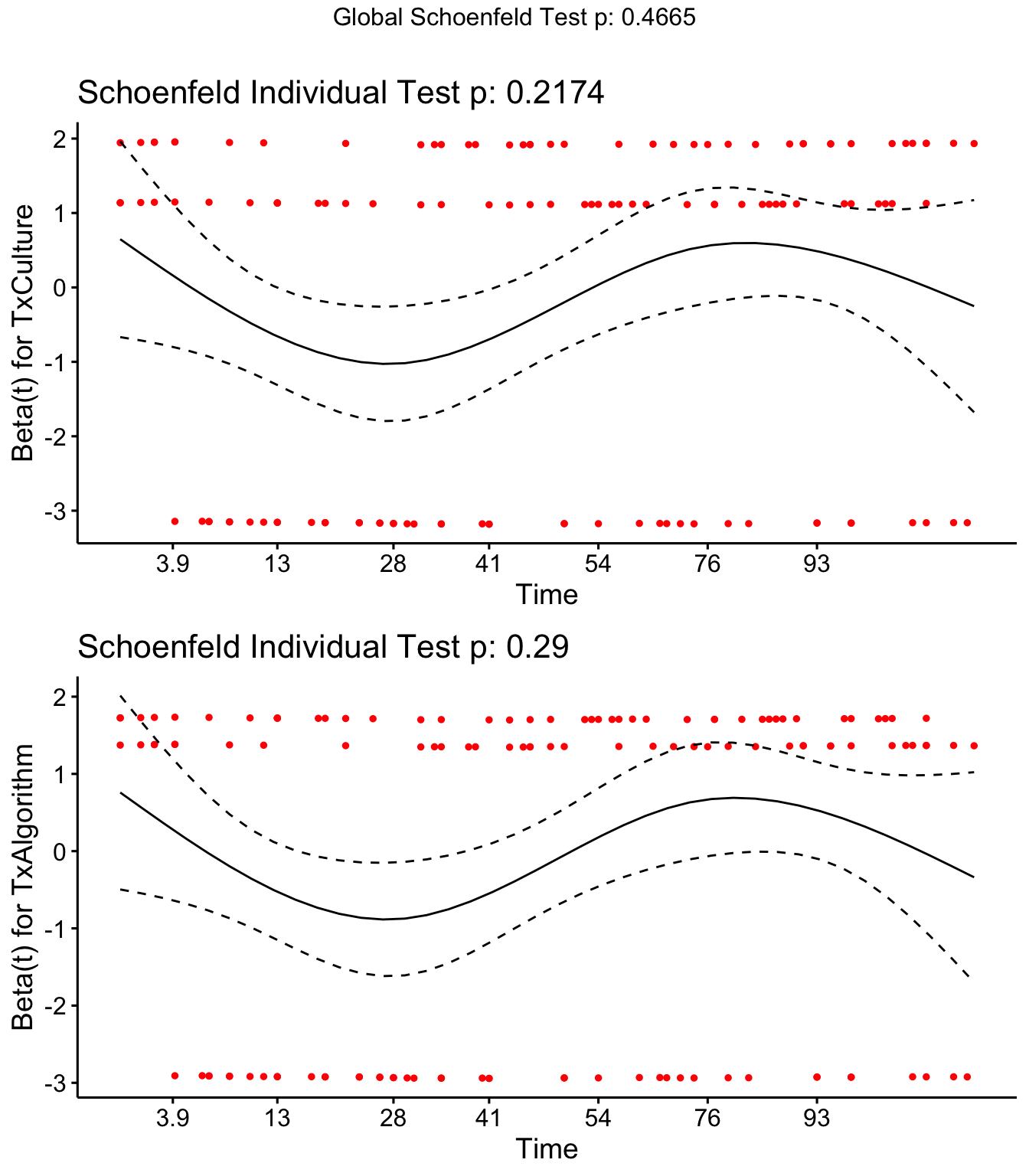

Step 7b: Final cox model for culling or death (1 - 120 DIM) using P-value based backwards stepwise selection

CoxCull <- coxph(Surv(CullTAR, Cull2) ~ Tx + Parity + DOSCC + PrevCM + cluster(FARMID), data=SDCTCOW) %>% tidy()
CoxCull$HR <- exp(CoxCull$estimate)
CoxCull$LCL <- exp(CoxCull$conf.low)
CoxCull$UCL <- exp(CoxCull$conf.high)
CoxCull <- CoxCull %>% select(term,HR,LCL,UCL,robust.se,p.value)
CoxCull

Estimates are similar to 10% rule based approach






Changing datasets: DHI dataset with multiple rows per cow

Dataset example

SDCTCOWDHI$Tx <- 
  factor(SDCTCOWDHI$Tx, 
         levels=c(0,1,2),
         labels=c("Blanket",
                  "Culture", 
                  "Algorithm"))

DHIcheck <- SDCTCOWDHI %>% select(Tx,CowID,FARMID,DIM,TestDIMcat20,LSCC,MY,Parity,PrevCM,DOMY,DOSCC)
head(DHIcheck, n=10)





Inspect data

DHIoutcome <- SDCTCOWDHI %>% select(SCC,MY,SCM)
DHIoutcome$logSCC <- log(DHIoutcome$SCC + 1)
#summarytools::dfSummary(DHIoutcome, style='grid')
print(summarytools::dfSummary(DHIoutcome, valid.col=FALSE, graph.magnif=0.8, varnumbers=F, style="grid"))
## Data Frame Summary  
##   
## Dimensions: 3992 x 4  
## Duplicates: 967  
## 
## +-----------+----------------------------+---------------------+------------------------+---------+
## | Variable  | Stats / Values             | Freqs (% of Valid)  | Graph                  | Missing |
## +===========+============================+=====================+========================+=========+
## | SCC       | Mean (sd) : 184.4 (678.2)  | 608 distinct values | :                      | 3       |
## | [numeric] | min < med < max:           |                     | :                      | (0.08%) |
## |           | 0 < 39 < 9999              |                     | :                      |         |
## |           | IQR (CV) : 89 (3.7)        |                     | :                      |         |
## |           |                            |                     | :                      |         |
## +-----------+----------------------------+---------------------+------------------------+---------+
## | MY        | Mean (sd) : 49.1 (10.5)    | 149 distinct values |         . :            | 2       |
## | [numeric] | min < med < max:           |                     |         : :            | (0.05%) |
## |           | 0.9 < 49.4 < 93.4          |                     |         : : :          |         |
## |           | IQR (CV) : 13.2 (0.2)      |                     |       . : : :          |         |
## |           |                            |                     |     . : : : : :        |         |
## +-----------+----------------------------+---------------------+------------------------+---------+
## | SCM       | Min  : 0                   | 0 : 3409 (85.5%)    | IIIIIIIIIIIIIIIII      | 3       |
## | [numeric] | Mean : 0.1                 | 1 :  580 (14.5%)    | II                     | (0.08%) |
## |           | Max  : 1                   |                     |                        |         |
## +-----------+----------------------------+---------------------+------------------------+---------+
## | logSCC    | Mean (sd) : 3.9 (1.4)      | 608 distinct values |       :                | 3       |
## | [numeric] | min < med < max:           |                     |       : .              | (0.08%) |
## |           | 0 < 3.7 < 9.2              |                     |     . : : .            |         |
## |           | IQR (CV) : 1.7 (0.3)       |                     |     : : : :            |         |
## |           |                            |                     |     : : : : : .        |         |
## +-----------+----------------------------+---------------------+------------------------+---------+

Very little missing data. Will do complete case analysis.



Assessing normality for continuous outcome variables

Somatic cell count (log x 10,000 cells)

library(qualityTools)
qqPlot(log(SDCTCOWDHI$SCC+1))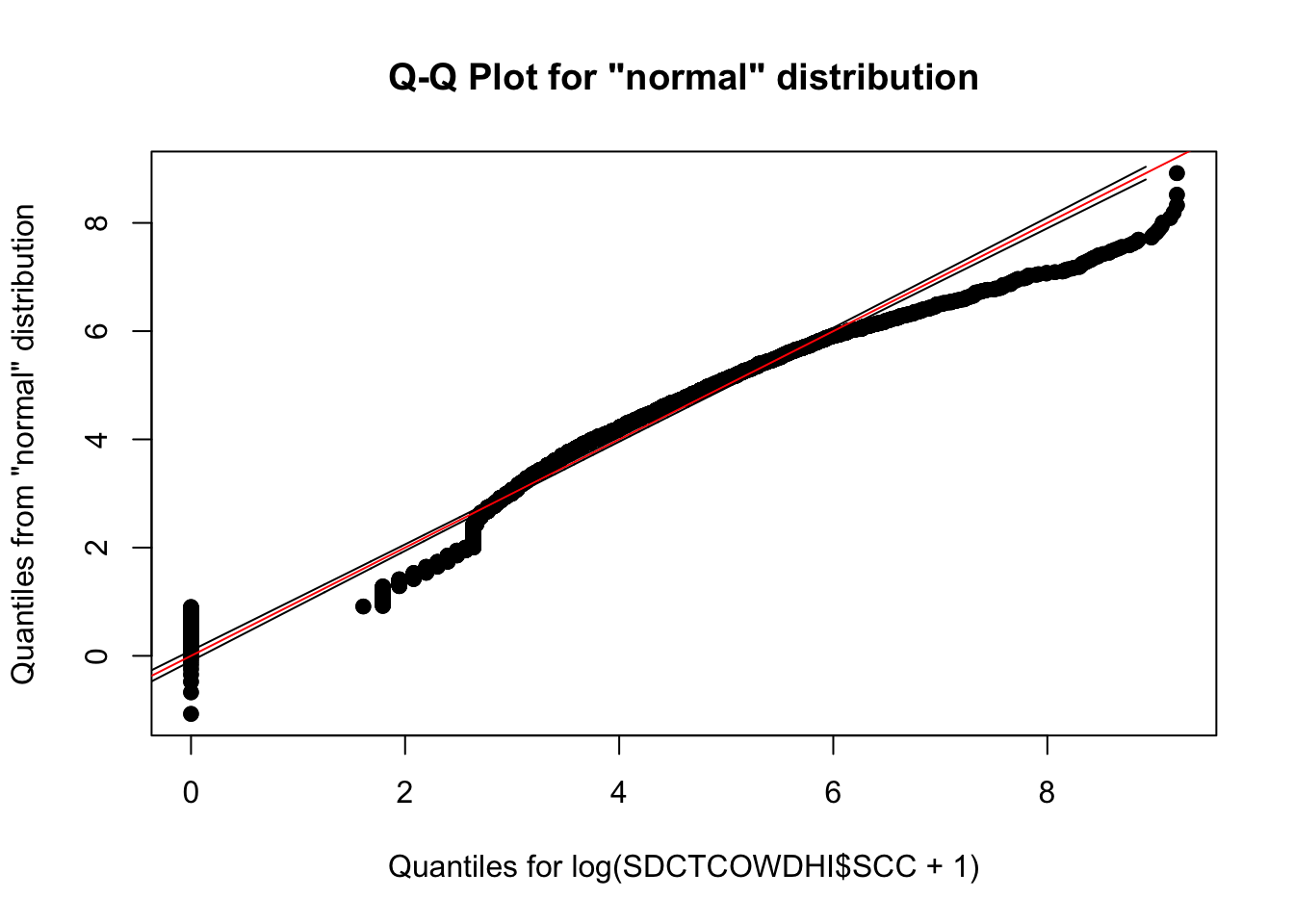

hist(log(SDCTCOWDHI$SCC+1))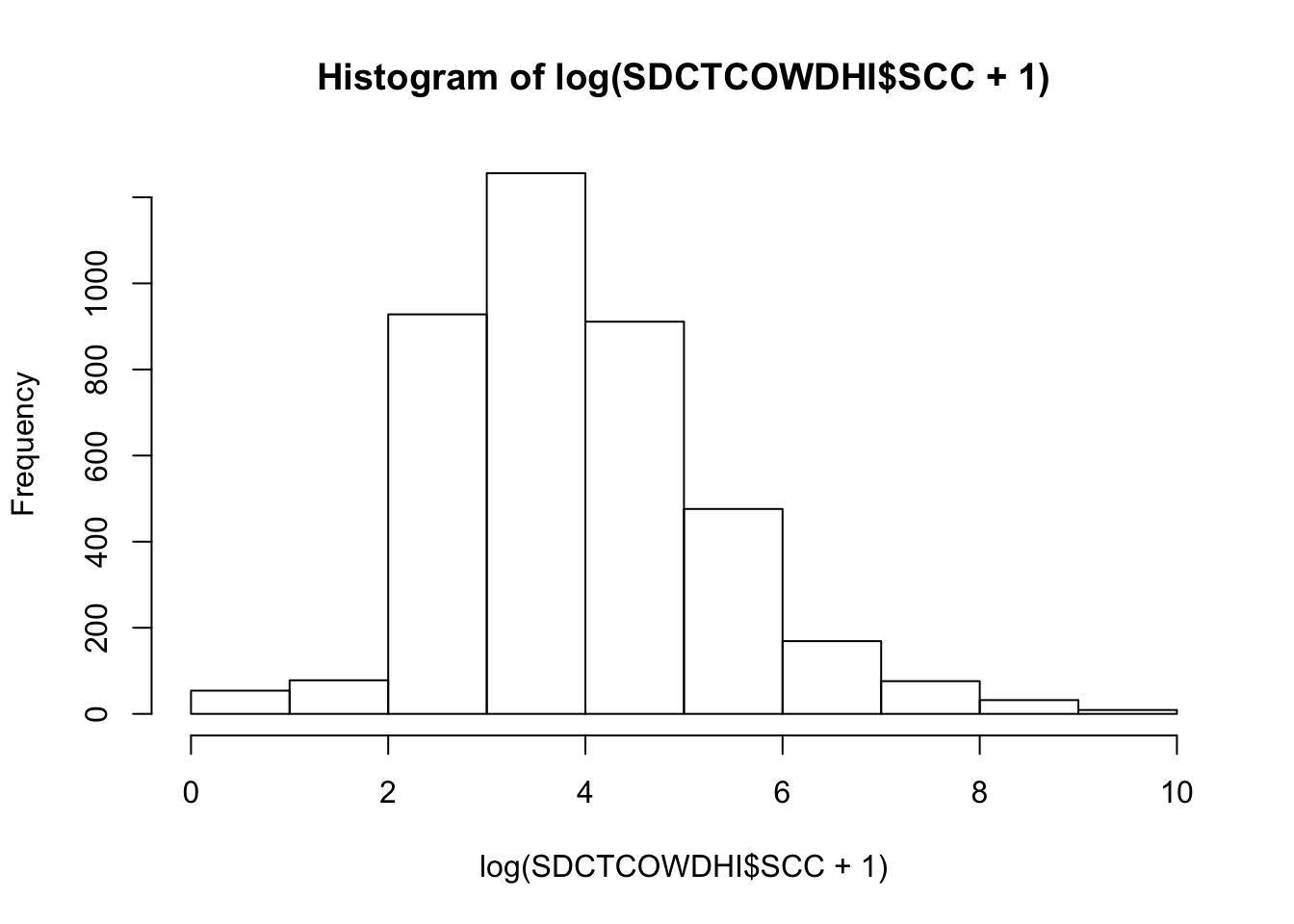





Milk yield (kg)

qqPlot(SDCTCOWDHI$MY)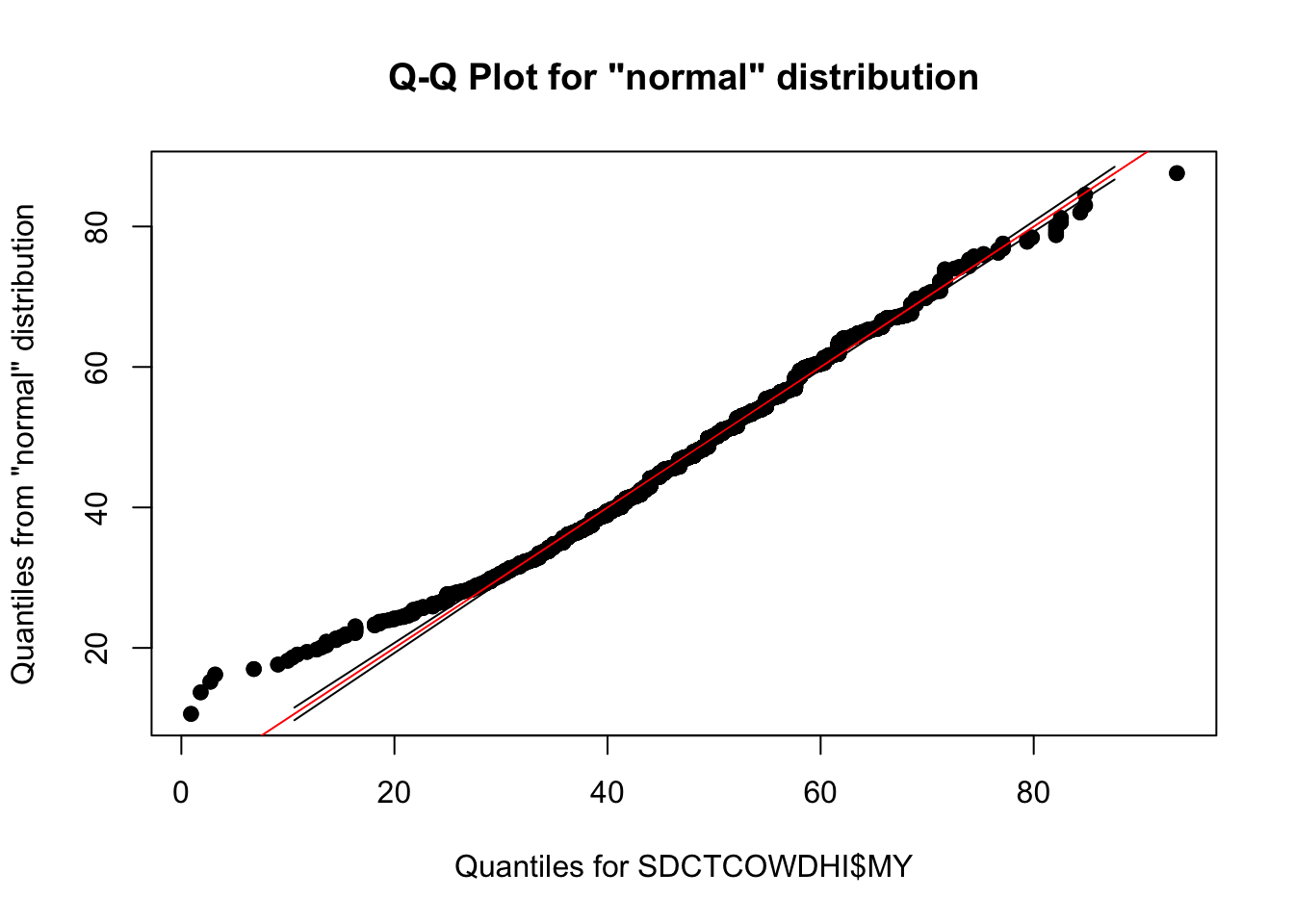

hist(SDCTCOWDHI$MY)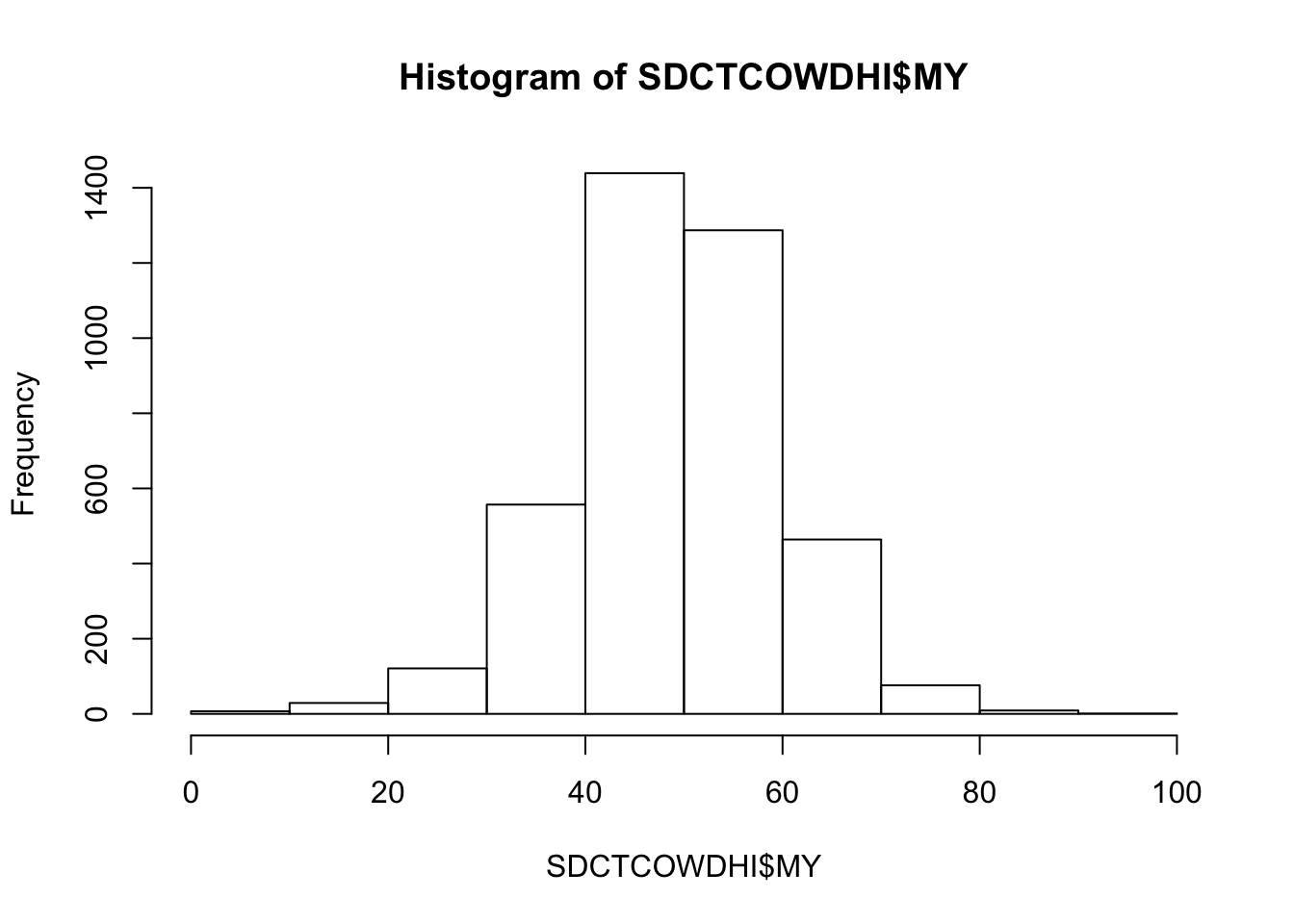





Outcome 3: Somatic cell count

Modelling plan

Model type: Linear mixed models, random intercepts for farm and cow will be fitted to account for repeated measures within cows, and clustering of cows within herds

Step 1: Identify potential confouders using a directed acyclic graph (DAG)

Step 2: Identify correlated variables using pearson and kendalls correlation coefficients

Step 3: Create model with all potential confounders

Step 4: Investigate potential effect measure modification

Step 5: Remove unneccesary covariates in backwards stepwise fashion using 10% rule (i.e. if estimated difference in SCC changes by >10% after removing the covariate, the covariate is retained in the model)

Step 6: Report final model

Step 7: Model diagnostics

Step 1 & 2 Identify potential confounders using a DAG

library(DiagrammeR)
mermaid("graph LR
        T(Treatment)-->U(SCC)
        A(Age)-->T
        P(Parity)-->T
        M(Yield at dry-off)-->T
        S(SCC during prev lactation)-->T
        C(CM in prev lact)-->T
        D(Days in milk at test)-->U
        D-->T
        A-->U
        P-->U
        M-->U
        S-->U
        C-->U
        C-->M
        P-->C
        P-->S
        P-->M
        A-->P
        A-->C
        A-->S
        A-->M
        M-->S
        C-->S
        style A fill:#FFFFFF, stroke-width:0px
        style T fill:#FFFFFF, stroke-width:2px
        style P fill:#FFFFFF, stroke-width:0px
        style M fill:#FFFFFF, stroke-width:0px
        style S fill:#FFFFFF, stroke-width:0px
        style C fill:#FFFFFF, stroke-width:0px
        style I fill:#FFFFFF, stroke-width:0px
        style D fill:#FFFFFF, stroke-width:0px
        style U fill:#FFFFFF, stroke-width:2px
        ")

According to this DAG, I may need to control for the following variables:

Parity [“Parity”] <- Age not offered as highly correlated

Yield at most recent test before dry off [“DOMY”]

Somatic cell count at last herd test during previous lactation [“DOSCC”] <- PrevSCCHI not offered as correlated

Clinical mastitis in previous lactation [“PrevCM”]

Days in milk at herd test (category, 0-20 “10”, 21-40 “30” etc) [“TestDIMcat20”]





Step 3: Create model with all potential confounders

library(lme4)
mm0 <- lmer(LSCC ~ Tx + TestDIMcat20 + Parity + DOSCC + DOMY + PrevCM + (1|FARMID/CowID), data=SDCTCOWDHI)
summary(mm0)
## Linear mixed model fit by REML ['lmerMod']
## Formula: LSCC ~ Tx + TestDIMcat20 + Parity + DOSCC + DOMY + PrevCM + (1 |  
##     FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 13110.3
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -5.5975 -0.4985 -0.1040  0.4340  3.9735 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 0.61791  0.7861  
##  FARMID       (Intercept) 0.02027  0.1424  
##  Residual                 1.14078  1.0681  
## Number of obs: 3989, groups:  CowID:FARMID, 1178; FARMID, 7
## 
## Fixed effects:
##                  Estimate Std. Error t value
## (Intercept)      3.338254   0.204372  16.334
## TxCulture        0.047878   0.070138   0.683
## TxAlgorithm      0.074745   0.070822   1.055
## TestDIMcat2030  -0.576961   0.063393  -9.101
## TestDIMcat2050  -0.557223   0.060950  -9.142
## TestDIMcat2070  -0.394721   0.059969  -6.582
## TestDIMcat2090  -0.272158   0.065089  -4.181
## TestDIMcat20110 -0.084757   0.060209  -1.408
## Parity2          0.110743   0.070611   1.568
## Parity3          0.259957   0.074986   3.467
## DOSCC            0.139922   0.028350   4.935
## DOMY             0.002402   0.003983   0.603
## PrevCM1          0.361076   0.087707   4.117
car::vif(mm0)
##                  GVIF Df GVIF^(1/(2*Df))
## Tx           1.009521  2        1.002372
## TestDIMcat20 1.003238  5        1.000323
## Parity       1.141466  2        1.033631
## DOSCC        1.319455  1        1.148676
## DOMY         1.167395  1        1.080461
## PrevCM       1.050427  1        1.024903





Step 4: Investigate effect measure modification

Tx:FARM (P > 0.05)

mm0 <- lmer(LSCC ~ Tx*FARMID + Parity + TestDIMcat20 + DOSCC + DOMY + PrevCM + (1|CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Tx:DIM category at herd test (P > 0.05)

mm0 <- lmer(LSCC ~ Tx*TestDIMcat20 + Parity + DOSCC + DOMY + PrevCM + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Tx:Parity (P > 0.05)

mm0 <- lmer(LSCC ~ Tx*Parity + TestDIMcat20 + DOSCC + DOMY + PrevCM + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Tx:PrevCM (P > 0.05)

mm0 <- lmer(LSCC ~ Tx*PrevCM + Parity + TestDIMcat20 + DOSCC + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Tx:DOMY (P > 0.05)

mm0 <- lmer(LSCC ~ Tx*DOMY + PrevCM + Parity + TestDIMcat20 + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)

Step 5: Remove unneccesary covariates in backwards stepwise fashion using 10% rule

The order for removing covariates will be in increasing likelihood of being a confounder, which is based on my knowledge about the variables and their distribution in treatment groups.

This order will be: DOMY, Parity, PrevCM, DOSCC

TestDIMcat20 will not be removed.

Step 5a: Full model

mm0 <- lmer(LSCC ~ Tx + PrevCM + Parity + TestDIMcat20 + DOSCC + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)
mm0 %>% tidy()





Step 5b: removing DOMY

mm0 <- lmer(LSCC ~ Tx + PrevCM + Parity + TestDIMcat20 + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI) 
mm0%>% tidy()

Changed by <10%. DOMY stays out.



Step 5b: removing Parity

mm0 <- lmer(LSCC ~ Tx + PrevCM + TestDIMcat20 + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI)
mm0 %>% tidy()

Changed by <10%. Parity stays out.





Step 5c: removing PrevCM

mm0 <- lmer(LSCC ~ Tx + TestDIMcat20 + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI) 
mm0 %>% tidy()

Changed by >10%. PrevCM stays in.



Step 5d: removing DOSCC

mm0 <- lmer(LSCC ~ Tx + PrevCM + TestDIMcat20 + (1|FARMID/CowID), data=SDCTCOWDHI)
mm0 %>% tidy()

Changed by > 10%. DOSCC stays in.



Step 6a: Final model for SCC (1 - 120 DIM)

mm0 <- lmer(LSCC ~ Tx + PrevCM + DOSCC + TestDIMcat20 + (1|FARMID/CowID), data=SDCTCOWDHI)
mm0 %>% tidy(conf.int=TRUE)

ICC for SCC (1 - 120 DIM)

mm0 <- lmer(LSCC ~ 1 + (1|FARMID/CowID), data=SDCTCOWDHI)
summary(mm0)
## Linear mixed model fit by REML ['lmerMod']
## Formula: LSCC ~ 1 + (1 | FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 13293.7
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -5.0159 -0.5107 -0.1062  0.4452  4.0999 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 0.65871  0.8116  
##  FARMID       (Intercept) 0.03917  0.1979  
##  Residual                 1.20343  1.0970  
## Number of obs: 3989, groups:  CowID:FARMID, 1178; FARMID, 7
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  3.86908    0.08308   46.57

ICC (CowID) = 0.35 ICC (FARMID) = 0.02

Most clustering is happening within cow (repeated measures).

Step 6b: Final model for SCC (1 - 120 DIM) using P-value based backwards selection

lmer(LSCC ~ Tx + Parity + PrevCM + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI) %>% summary()
## Linear mixed model fit by REML ['lmerMod']
## Formula: LSCC ~ Tx + Parity + PrevCM + DOSCC + (1 | FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 13233.2
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -5.1671 -0.5100 -0.1122  0.4512  4.1458 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 0.59501  0.7714  
##  FARMID       (Intercept) 0.01825  0.1351  
##  Residual                 1.20377  1.0972  
## Number of obs: 3989, groups:  CowID:FARMID, 1178; FARMID, 7
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  3.12018    0.13160  23.710
## TxCulture    0.04063    0.06986   0.582
## TxAlgorithm  0.06227    0.07063   0.882
## Parity2      0.11211    0.07042   1.592
## Parity3      0.25300    0.07477   3.384
## PrevCM1      0.37041    0.08730   4.243
## DOSCC        0.13267    0.02635   5.035
## 
## Correlation of Fixed Effects:
##             (Intr) TxCltr TxAlgr Party2 Party3 PrvCM1
## TxCulture   -0.298                                   
## TxAlgorithm -0.270  0.498                            
## Parity2     -0.042  0.054  0.021                     
## Parity3      0.038  0.012  0.019  0.439              
## PrevCM1      0.069 -0.019  0.013 -0.044 -0.100       
## DOSCC       -0.786  0.026  0.000 -0.223 -0.295 -0.143
lmer(LSCC ~ Tx + Parity + PrevCM + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI) %>% car::Anova() %>% tidy()

Estimates are very similar to 10% rule based approach.



Step 6c: Final model (using 10% rule) reported as estimated marginal means (~LSmeans)

Mean log SCC

library(emmeans)
mm0 <- lmer(LSCC ~ Tx + PrevCM + DOSCC + TestDIMcat20 + (1|FARMID/CowID), data=SDCTCOWDHI)
emm <- emmeans(mm0, ~Tx) %>% tidy()
emm

Step 6c: Final model (using 10% rule) reported as back-transformed estimated marginal means (~LSmeans)

Geometric mean SCC

mm0 <- lmer(LSCC ~ Tx + PrevCM + DOSCC + TestDIMcat20 + (1|FARMID/CowID), data=SDCTCOWDHI)
emm <- emmeans(mm0, ~Tx) %>% tidy()
emm$SCC <- exp(emm$estimate) 
emm$LCL <- exp(emm$asymp.LCL)
emm$UCL <- exp(emm$asymp.UCL)
emm <- emm %>% subset(select=c(Tx,SCC,LCL,UCL))
emm




Reported as back-transformed estimated marginal means by herd test day, no interaction with test DIM

mm0 <- lmer(LSCC ~ Tx + TestDIMcat20 + DOSCC + PrevCM + (1|FARMID/CowID), data=SDCTCOWDHI)
atx <- c(10,30,50,70,90,110)
emm <- emmeans(mm0, ~Tx*TestDIMcat20, at=list(atx)) %>% tidy()
emm$SCC <- exp(emm$estimate)
emm$LCL <- exp(emm$asymp.LCL)
emm$UCL <- exp(emm$asymp.UCL)
emm <- emm %>% subset(select=c(Tx,TestDIMcat20,SCC,LCL,UCL))
curve <- ggplot(emm) + coord_cartesian(ylim = (c(0,100))) + aes(x=TestDIMcat20, y=SCC, group=Tx, colour=Tx) + geom_point() + geom_line(aes(colour=Tx,linetype=Tx)) + geom_ribbon(aes(ymin=emm$LCL, ymax=emm$UCL,colour=Tx,fill=Tx), linetype=0, alpha=0.1)
curve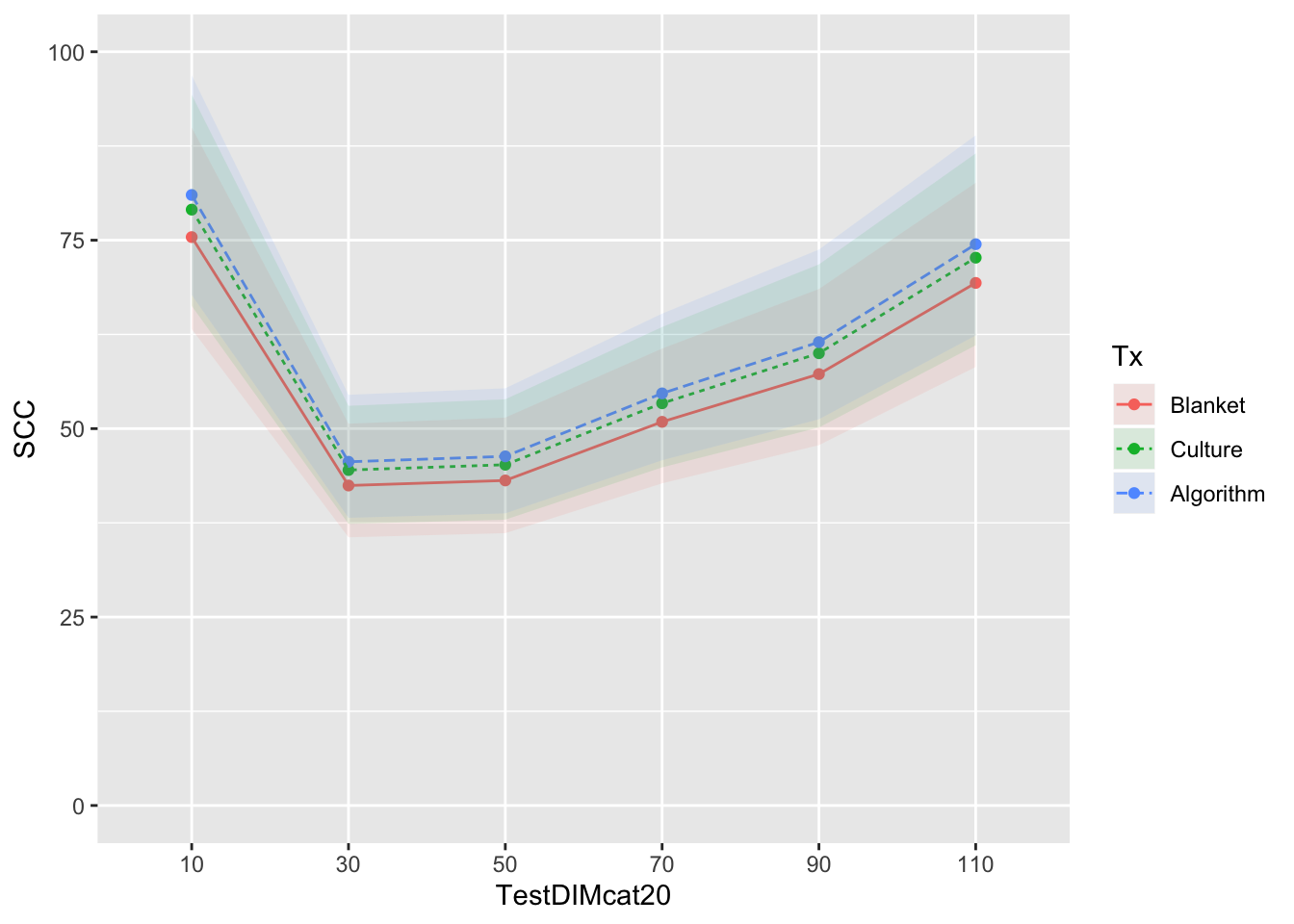





Reported as back-transformed estimated marginal means by herd test day, with interaction with test DIM

mm0 <- lmer(LSCC ~ Tx*TestDIMcat20 + PrevCM + DOSCC + (1|FARMID/CowID), data=SDCTCOWDHI)
atx <- c(10,30,50,70,90,110)
emm <- emmeans(mm0, ~Tx*TestDIMcat20, at=list(atx)) %>% tidy()
emm$SCC <- exp(emm$estimate)
emm$LCL <- exp(emm$asymp.LCL)
emm$UCL <- exp(emm$asymp.UCL)
emm <- emm %>% subset(select=c(Tx,TestDIMcat20,SCC,LCL,UCL))
curve <- ggplot(emm) + coord_cartesian(ylim = (c(0,100))) + aes(x=TestDIMcat20, y=SCC, group=Tx, colour=Tx) + geom_point() + geom_line(aes(colour=Tx,linetype=Tx)) + geom_ribbon(aes(ymin=emm$LCL, ymax=emm$UCL,colour=Tx,fill=Tx), linetype=0, alpha=0.1)
curve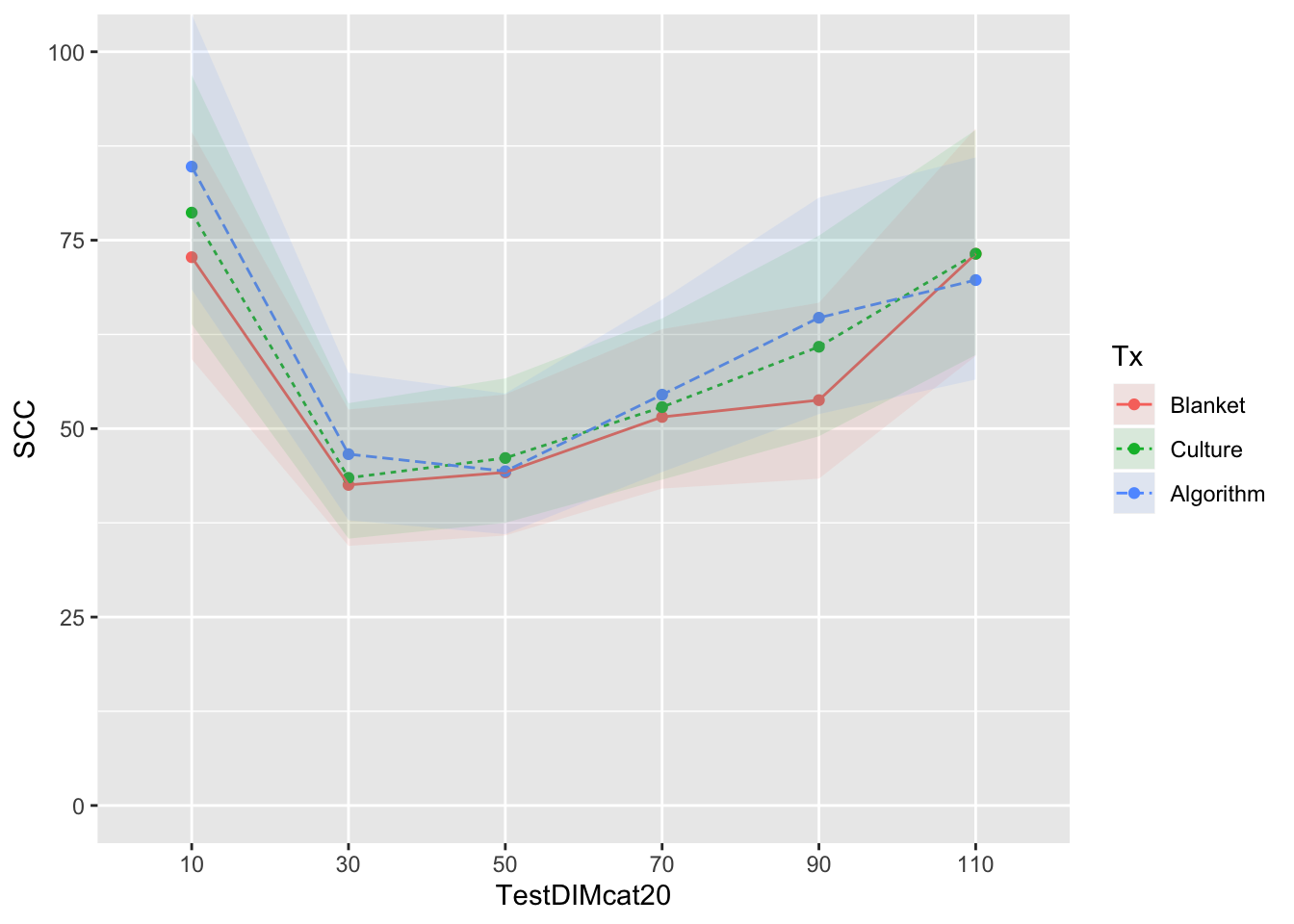





Step 7: Model diagnostics

Checking homoskedasticity assumption (variance of residuals)

mm0 <- lmer(LSCC ~ Tx + TestDIMcat20 + (1|FARMID/CowID), data=SDCTCOWDHI)
ggplot(data.frame(eta=predict(mm0,type="link"),pearson=residuals(mm0,type="pearson")),
       aes(x=eta,y=pearson)) +
  geom_point() +
  theme_bw()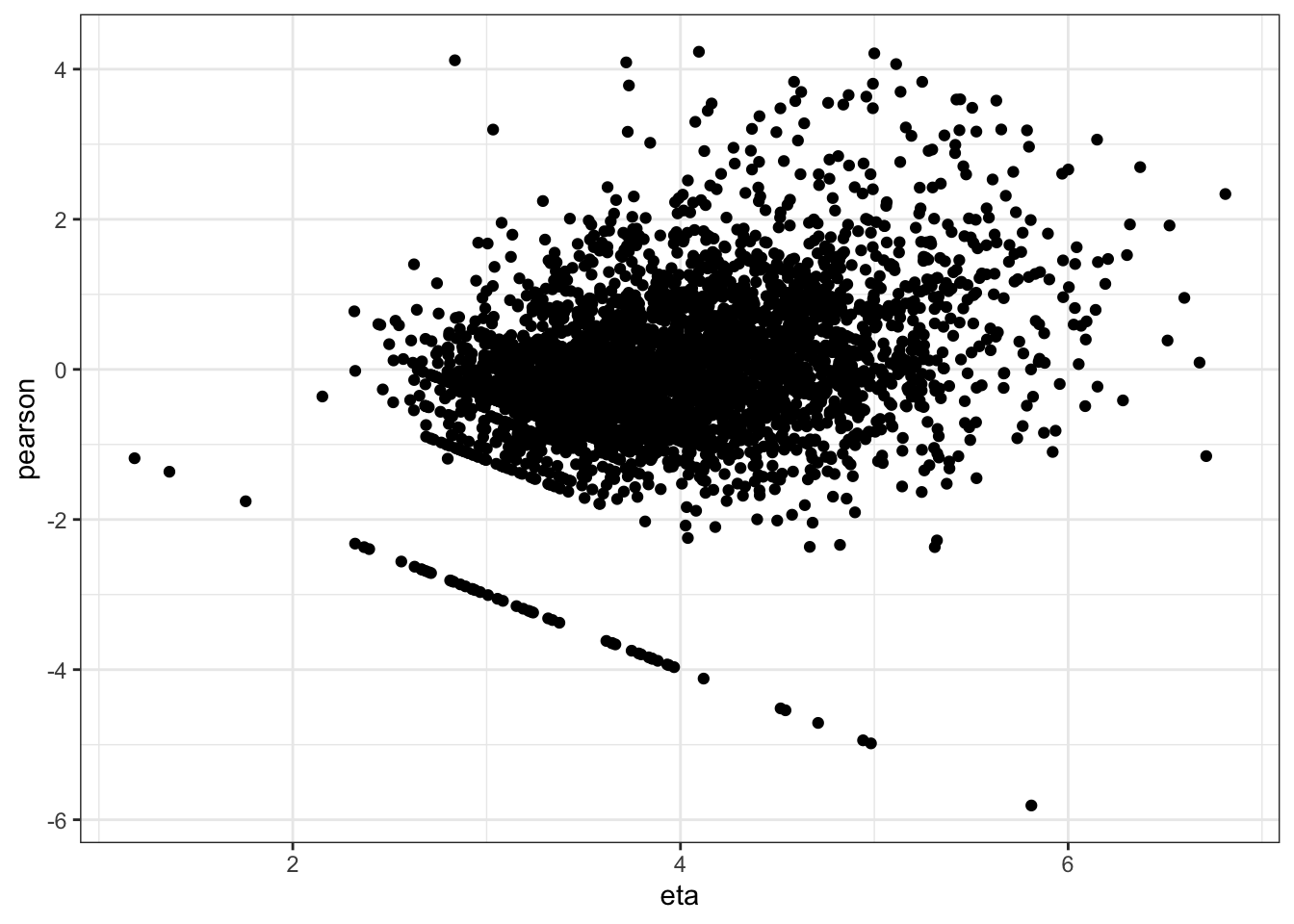

Checking normality of residuals

qqnorm(residuals(mm0))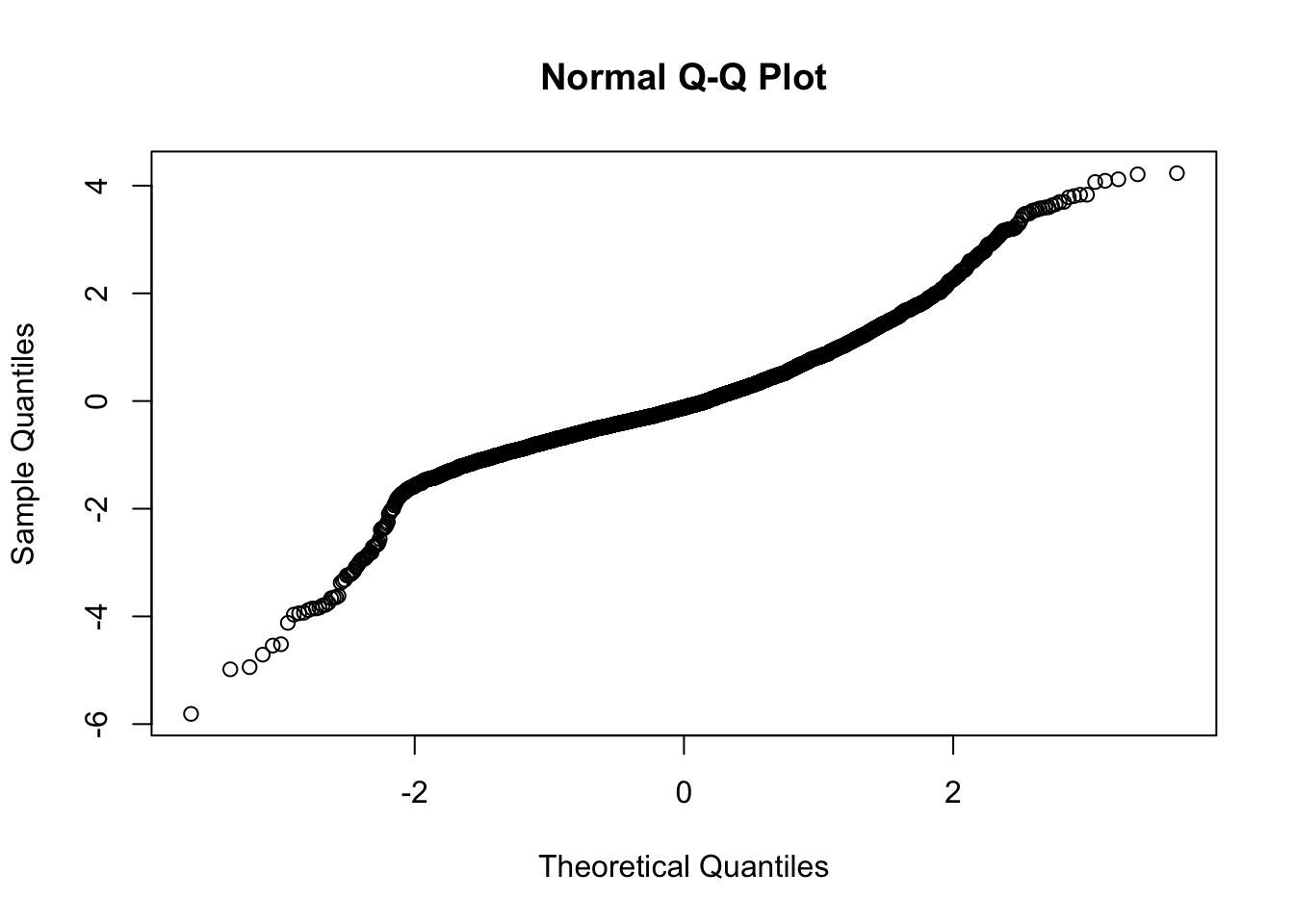

Evidence of small L tail. Although some evidence of heteroskedasticity and not perfectly normal residuals, I believe these are allowable for this model.

Outcome 4: Milk yield

Modelling plan

Model type: Linear mixed models, random intercepts for farm and cow will be fitted to account for repeated measures within cows, and clustering of cows within herds

Step 1: Identify potential confouders using a directed acyclic graph (DAG)

Step 2: Identify correlated variables using pearson and kendalls correlation coefficients

Step 3: Create model with all potential confounders

Step 4: Investigate potential effect measure modification

Step 5: Remove unneccesary covariates in backwards stepwise fashion using 10% rule (i.e. if estimated difference in milk yield changes by >10% after removing the covariate, the covariate is retained in the model)

Step 6: Report final model

Step 7: Model diagnostics

Step 1 & 2 Identify potential confounders using a DAG

library(DiagrammeR)
mermaid("graph LR
        T(Treatment)-->U(Milk yield)
        A(Age)-->T
        P(Parity)-->T
        M(Yield at dry-off)-->T
        S(SCC during prev lactation)-->T
        C(CM in prev lact)-->T
        D(Days in milk at test)-->U
        D-->T
        A-->U
        P-->U
        M-->U
        S-->U
        C-->U
        C-->M
        P-->C
        P-->S
        P-->M
        A-->P
        A-->C
        A-->S
        A-->M
        M-->S
        C-->S
        style A fill:#FFFFFF, stroke-width:0px
        style T fill:#FFFFFF, stroke-width:2px
        style P fill:#FFFFFF, stroke-width:0px
        style M fill:#FFFFFF, stroke-width:0px
        style S fill:#FFFFFF, stroke-width:0px
        style C fill:#FFFFFF, stroke-width:0px
        style I fill:#FFFFFF, stroke-width:0px
        style D fill:#FFFFFF, stroke-width:0px
        style U fill:#FFFFFF, stroke-width:2px
        ")

According to this DAG, I may need to control for the following variables:

Parity [“Parity”] <- Age not offered as highly correlated

Yield at most recent test before dry off [“DOMY”]

Somatic cell count at last herd test during previous lactation [“DOSCC”] <- PrevSCCHI not offered as correlated

Clinical mastitis in previous lactation [“PrevCM”]

Days in milk at herd test (category, 0-20 “10”, 21-40 “30” etc) [“TestDIMcat20”]





Step 3: Create a model with all potential covariates

mm0 <- lmer(MY ~ Tx + TestDIMcat20 + Parity + DOSCC + PrevCM + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)
summary(mm0)
## Linear mixed model fit by REML ['lmerMod']
## Formula: MY ~ Tx + TestDIMcat20 + Parity + DOSCC + PrevCM + DOMY + (1 |  
##     FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 27948.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -6.3698 -0.4620  0.0223  0.5283  3.9851 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 28.70    5.357   
##  FARMID       (Intercept)  9.63    3.103   
##  Residual                 46.18    6.795   
## Number of obs: 3990, groups:  CowID:FARMID, 1177; FARMID, 7
## 
## Fixed effects:
##                 Estimate Std. Error t value
## (Intercept)     30.22473    1.76719  17.103
## TxCulture       -0.04144    0.46718  -0.089
## TxAlgorithm     -0.92795    0.47146  -1.968
## TestDIMcat2030  11.86182    0.40548  29.253
## TestDIMcat2050  12.87916    0.38854  33.148
## TestDIMcat2070  12.51208    0.38249  32.713
## TestDIMcat2090  11.01316    0.41572  26.492
## TestDIMcat20110  8.43431    0.38401  21.964
## Parity2          2.52549    0.47112   5.361
## Parity3          3.01851    0.50067   6.029
## DOSCC            0.26481    0.19029   1.392
## PrevCM1         -0.24232    0.58620  -0.413
## DOMY             0.22068    0.02706   8.156
car::vif(mm0)
##                  GVIF Df GVIF^(1/(2*Df))
## Tx           1.009493  2        1.002365
## TestDIMcat20 1.002987  5        1.000298
## Parity       1.145893  2        1.034632
## DOSCC        1.308164  1        1.143750
## PrevCM       1.048252  1        1.023842
## DOMY         1.154875  1        1.074651





Step 4: Investigate effect measure modification

Tx:FARM (P < 0.05)

mm0 <- lmer(MY ~ Tx*FARMID + Parity + TestDIMcat20 + DOSCC + DOMY + PrevCM + (1|CowID), data=SDCTCOWDHI)
car::Anova(mm0)

Significant interaction term.

Descision: Revisit this after covariates are finalized.



Tx:DIM category at herd test (P > 0.05)

mm0 <- lmer(MY ~ Tx*TestDIMcat20 + Parity + DOSCC + DOMY + PrevCM + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Tx:Parity (P > 0.05)

mm0 <- lmer(MY ~ Tx*Parity + TestDIMcat20 + DOSCC + DOMY + PrevCM + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Tx:PrevCM (P > 0.05)

mm0 <- lmer(MY ~ Tx*PrevCM + Parity + TestDIMcat20 + DOSCC + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)
car::Anova(mm0)





Step 5: Remove unnecessary covariates using backwards selection (10% rule)

The order for removing covariates will be in increasing likelihood of being a confounder, which is based on my knowledge about the variables and their distribution in treatment groups.

This order will be: DOSCC, PrevCM, Parity, DOMY

TestDIMcat20 will not be removed (forced into model).

Step 5a: Full model

mm0 <- lmer(MY ~ Tx + PrevCM + Parity + TestDIMcat20 + DOSCC + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI) 
mm0 %>% tidy() %>% subset(select=c(term,estimate))





Step 5b: Removing DOSCC

mm0 <- lmer(MY ~ Tx + PrevCM + Parity + TestDIMcat20 + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI) 
mm0 %>% tidy() %>% subset(select=c(term,estimate))

Changed by <10%. DOSCC stays out



Step 5c: removing PrevCM

mm0 <- lmer(MY ~ Tx + Parity + TestDIMcat20 + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)  
mm0 %>% tidy() %>% subset(select=c(term,estimate))

Changed by < 10%. PrevCM stays out.





Step 5d: removing Parity

mm0 <- lmer(MY ~ Tx + TestDIMcat20 + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI) 
mm0 %>% tidy() %>% subset(select=c(term,estimate))

Changed by >10%. Parity stays in.


Step 5e: removing DOMY

mm0 <- lmer(MY ~ Tx + Parity + TestDIMcat20 + (1|FARMID/CowID), data=SDCTCOWDHI) 
mm0 %>% tidy() %>% subset(select=c(term,estimate))

Changed by >10%. DOMY stays in.



Revisit effect measure modification previously identified

Effect measure modification with herd (P < 0.05)

mm0 <- lmer(MY ~ Tx*FARMID + TestDIMcat20 + Parity + DOMY + (1|CowID), data=SDCTCOWDHI)
car::Anova(mm0)

Decision - will investigate effect estimates stratified by herd



Step 6a: Final model for milk yield (1 - 120 DIM), stratified by herd.

Model output

mm0 <- lmer(MY ~ Tx*FARMID + TestDIMcat20 + Parity + DOMY + (1|CowID), data=SDCTCOWDHI)
emmeans(mm0,pairwise ~ Tx | FARMID)
## $emmeans
## FARMID = 1:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     47.4 1.240 Inf      45.0      49.8
##  Culture     49.7 1.162 Inf      47.4      51.9
##  Algorithm   46.2 1.381 Inf      43.5      48.9
## 
## FARMID = 2:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     49.6 1.200 Inf      47.3      52.0
##  Culture     46.0 1.300 Inf      43.4      48.5
##  Algorithm   43.4 1.188 Inf      41.1      45.8
## 
## FARMID = 3:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     43.4 0.703 Inf      42.1      44.8
##  Culture     43.8 0.701 Inf      42.4      45.1
##  Algorithm   42.0 0.736 Inf      40.6      43.5
## 
## FARMID = 4:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     53.3 0.565 Inf      52.2      54.4
##  Culture     52.5 0.534 Inf      51.4      53.5
##  Algorithm   53.2 0.558 Inf      52.2      54.3
## 
## FARMID = 5:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     49.4 0.739 Inf      48.0      50.9
##  Culture     49.9 0.712 Inf      48.5      51.3
##  Algorithm   48.1 0.752 Inf      46.6      49.5
## 
## FARMID = 6:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     49.2 1.515 Inf      46.2      52.1
##  Culture     52.3 1.548 Inf      49.2      55.3
##  Algorithm   50.7 1.698 Inf      47.4      54.1
## 
## FARMID = 7:
##  Tx        emmean    SE  df asymp.LCL asymp.UCL
##  Blanket     50.4 1.014 Inf      48.4      52.4
##  Culture     49.4 1.066 Inf      47.3      51.5
##  Algorithm   49.2 1.067 Inf      47.1      51.2
## 
## Results are averaged over the levels of: TestDIMcat20, Parity 
## Degrees-of-freedom method: asymptotic 
## Confidence level used: 0.95 
## 
## $contrasts
## FARMID = 1:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture    -2.2771 1.693 Inf -1.345  0.3704 
##  Blanket - Algorithm   1.1734 1.848 Inf  0.635  0.8008 
##  Culture - Algorithm   3.4506 1.800 Inf  1.917  0.1337 
## 
## FARMID = 2:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture     3.6627 1.767 Inf  2.072  0.0956 
##  Blanket - Algorithm   6.2020 1.686 Inf  3.678  0.0007 
##  Culture - Algorithm   2.5393 1.758 Inf  1.444  0.3182 
## 
## FARMID = 3:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture    -0.3310 0.990 Inf -0.334  0.9402 
##  Blanket - Algorithm   1.4086 1.015 Inf  1.388  0.3474 
##  Culture - Algorithm   1.7396 1.015 Inf  1.713  0.2002 
## 
## FARMID = 4:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture     0.8679 0.770 Inf  1.128  0.4969 
##  Blanket - Algorithm   0.0873 0.786 Inf  0.111  0.9932 
##  Culture - Algorithm  -0.7806 0.760 Inf -1.027  0.5600 
## 
## FARMID = 5:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture    -0.5102 0.985 Inf -0.518  0.8627 
##  Blanket - Algorithm   1.3592 1.015 Inf  1.339  0.3733 
##  Culture - Algorithm   1.8695 1.003 Inf  1.863  0.1495 
## 
## FARMID = 6:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture    -3.1044 2.164 Inf -1.435  0.3229 
##  Blanket - Algorithm  -1.5474 2.273 Inf -0.681  0.7747 
##  Culture - Algorithm   1.5571 2.290 Inf  0.680  0.7753 
## 
## FARMID = 7:
##  contrast            estimate    SE  df z.ratio p.value
##  Blanket - Culture     0.9515 1.467 Inf  0.649  0.7931 
##  Blanket - Algorithm   1.2379 1.468 Inf  0.843  0.6761 
##  Culture - Algorithm   0.2864 1.503 Inf  0.191  0.9802 
## 
## Results are averaged over the levels of: TestDIMcat20, Parity 
## P value adjustment: tukey method for comparing a family of 3 estimates

It appears that herd 2 (87 cows) and herd 6 (42 cows) have extreme results compared with the other herds. In herd 2, BDCT had much higher MY than SDCT cows. In herd 6, it was the opposite effect. Given these were the smallest herds in the study, I will report a pooled result.



Step 6bi: Final model reported without herd interaction

Model output

summary(lmer(MY ~ Tx + TestDIMcat20 + Parity + DOMY+ (1|FARMID/CowID), data=SDCTCOWDHI))
## Linear mixed model fit by REML ['lmerMod']
## Formula: MY ~ Tx + TestDIMcat20 + Parity + DOMY + (1 | FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 27949.8
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -6.3374 -0.4572  0.0207  0.5284  3.9942 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 28.677   5.355   
##  FARMID       (Intercept)  9.946   3.154   
##  Residual                 46.184   6.796   
## Number of obs: 3990, groups:  CowID:FARMID, 1177; FARMID, 7
## 
## Fixed effects:
##                 Estimate Std. Error t value
## (Intercept)     31.61485    1.47112  21.490
## TxCulture       -0.04671    0.46702  -0.100
## TxAlgorithm     -0.92025    0.47129  -1.953
## TestDIMcat2030  11.86555    0.40548  29.263
## TestDIMcat2050  12.87773    0.38856  33.143
## TestDIMcat2070  12.51168    0.38250  32.710
## TestDIMcat2090  11.01773    0.41571  26.503
## TestDIMcat20110  8.43423    0.38402  21.963
## Parity2          2.66366    0.45780   5.818
## Parity3          3.20325    0.47445   6.752
## DOMY             0.20758    0.02539   8.175
## 
## Correlation of Fixed Effects:
##             (Intr) TxCltr TxAlgr TDIM203 TDIM205 TDIM207 TDIM209 TDIM201
## TxCulture   -0.132                                                      
## TxAlgorithm -0.146  0.499                                               
## TstDIMc2030 -0.144 -0.013 -0.012                                        
## TstDIMc2050 -0.132 -0.010 -0.013  0.486                                 
## TstDIMc2070 -0.135 -0.010 -0.004  0.534   0.481                         
## TstDIMc2090 -0.143 -0.005 -0.005  0.515   0.499   0.471                 
## TstDIM20110 -0.129 -0.008 -0.004  0.514   0.507   0.527   0.465         
## Parity2     -0.167  0.055  0.021  0.000   0.008  -0.001   0.004   0.006 
## Parity3     -0.173  0.013  0.018 -0.014   0.009  -0.009   0.012  -0.001 
## DOMY        -0.478 -0.065 -0.027  0.013  -0.002  -0.002   0.019  -0.014 
##             Party2 Party3
## TxCulture                
## TxAlgorithm              
## TstDIMc2030              
## TstDIMc2050              
## TstDIMc2070              
## TstDIMc2090              
## TstDIM20110              
## Parity2                  
## Parity3      0.399       
## DOMY         0.066  0.101

Model output (tidy)

lmer(MY ~ Tx + TestDIMcat20 + Parity + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI) %>% tidy(conf.int=TRUE)

ICC for MY (1 - 120 DIM)

mm0 <- lmer(MY ~ 1 + (1|FARMID/CowID), data=SDCTCOWDHI)
summary(mm0)
## Linear mixed model fit by REML ['lmerMod']
## Formula: MY ~ 1 + (1 | FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 29310.2
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -5.1211 -0.4867  0.0849  0.5681  3.5617 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 27.03    5.199   
##  FARMID       (Intercept) 10.06    3.172   
##  Residual                 70.88    8.419   
## Number of obs: 3990, groups:  CowID:FARMID, 1177; FARMID, 7
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   48.286      1.226   39.38

ICC (CowID) = 0.25 ICC (FARMID) = 0.09

Emmeans without TestDIM interaction

mm0 <- lmer(MY ~ Tx + TestDIMcat20 + Parity + DOMY+ (1|FARMID/CowID), data=SDCTCOWDHI)

emmeans(mm0,~Tx) %>% tidy

Step 6bii: Final model reported without herd interaction (using P-value based backwards elimination)

Model output

summary(lmer(MY ~ Tx + TestDIMcat20 + Parity + (1|FARMID/CowID), data=SDCTCOWDHI))
## Linear mixed model fit by REML ['lmerMod']
## Formula: MY ~ Tx + TestDIMcat20 + Parity + (1 | FARMID/CowID)
##    Data: SDCTCOWDHI
## 
## REML criterion at convergence: 28009.3
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -6.2353 -0.4645  0.0246  0.5246  3.9839 
## 
## Random effects:
##  Groups       Name        Variance Std.Dev.
##  CowID:FARMID (Intercept) 31.11    5.578   
##  FARMID       (Intercept) 11.14    3.338   
##  Residual                 46.17    6.795   
## Number of obs: 3990, groups:  CowID:FARMID, 1177; FARMID, 7
## 
## Fixed effects:
##                 Estimate Std. Error t value
## (Intercept)      37.3558     1.3606  27.456
## TxCulture         0.2008     0.4792   0.419
## TxAlgorithm      -0.8169     0.4844  -1.687
## TestDIMcat2030   11.8422     0.4064  29.139
## TestDIMcat2050   12.8803     0.3890  33.113
## TestDIMcat2070   12.5248     0.3830  32.704
## TestDIMcat2090   10.9596     0.4165  26.315
## TestDIMcat20110   8.4713     0.3844  22.040
## Parity2           2.4166     0.4697   5.145
## Parity3           2.8034     0.4853   5.777
## 
## Correlation of Fixed Effects:
##             (Intr) TxCltr TxAlgr TDIM203 TDIM205 TDIM207 TDIM209 TDIM201
## TxCulture   -0.182                                                      
## TxAlgorithm -0.177  0.499                                               
## TstDIMc2030 -0.150 -0.012 -0.012                                        
## TstDIMc2050 -0.144 -0.010 -0.013  0.486                                 
## TstDIMc2070 -0.147 -0.010 -0.004  0.535   0.480                         
## TstDIMc2090 -0.145 -0.004 -0.005  0.515   0.499   0.470                 
## TstDIM20110 -0.147 -0.009 -0.005  0.515   0.507   0.528   0.464         
## Parity2     -0.151  0.059  0.022 -0.001   0.008  -0.001   0.003   0.006 
## Parity3     -0.139  0.019  0.021 -0.015   0.009  -0.008   0.010   0.000 
##             Party2
## TxCulture         
## TxAlgorithm       
## TstDIMc2030       
## TstDIMc2050       
## TstDIMc2070       
## TstDIMc2090       
## TstDIM20110       
## Parity2           
## Parity3      0.395





Step 6biii: Final model (using 10% rule) reported as estimated marginal means by test DIM category (no interaction with test DIM)

mm0 <- lmer(MY ~ Tx + TestDIMcat20 + Parity + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)

atx <- c(10,30,50,70,90,110)
emm <- emmeans(mm0, ~Tx*TestDIMcat20) %>% tidy()
emm$MY <- emm$estimate
emm$LCL <- emm$asymp.LCL
emm$UCL <- emm$asymp.UCL
emm %>% subset(select=c(Tx,TestDIMcat20,MY,LCL,UCL))

Plotting model as predicted values

curve <- ggplot(emm) + coord_cartesian(ylim = (c(0,55))) + aes(x=TestDIMcat20, y=MY, group=Tx, colour=Tx) + geom_point() + geom_line(aes(colour=Tx,linetype=Tx)) + geom_ribbon(aes(ymin=emm$LCL, ymax=emm$UCL,colour=Tx,fill=Tx), linetype=0, alpha=0.1)
curve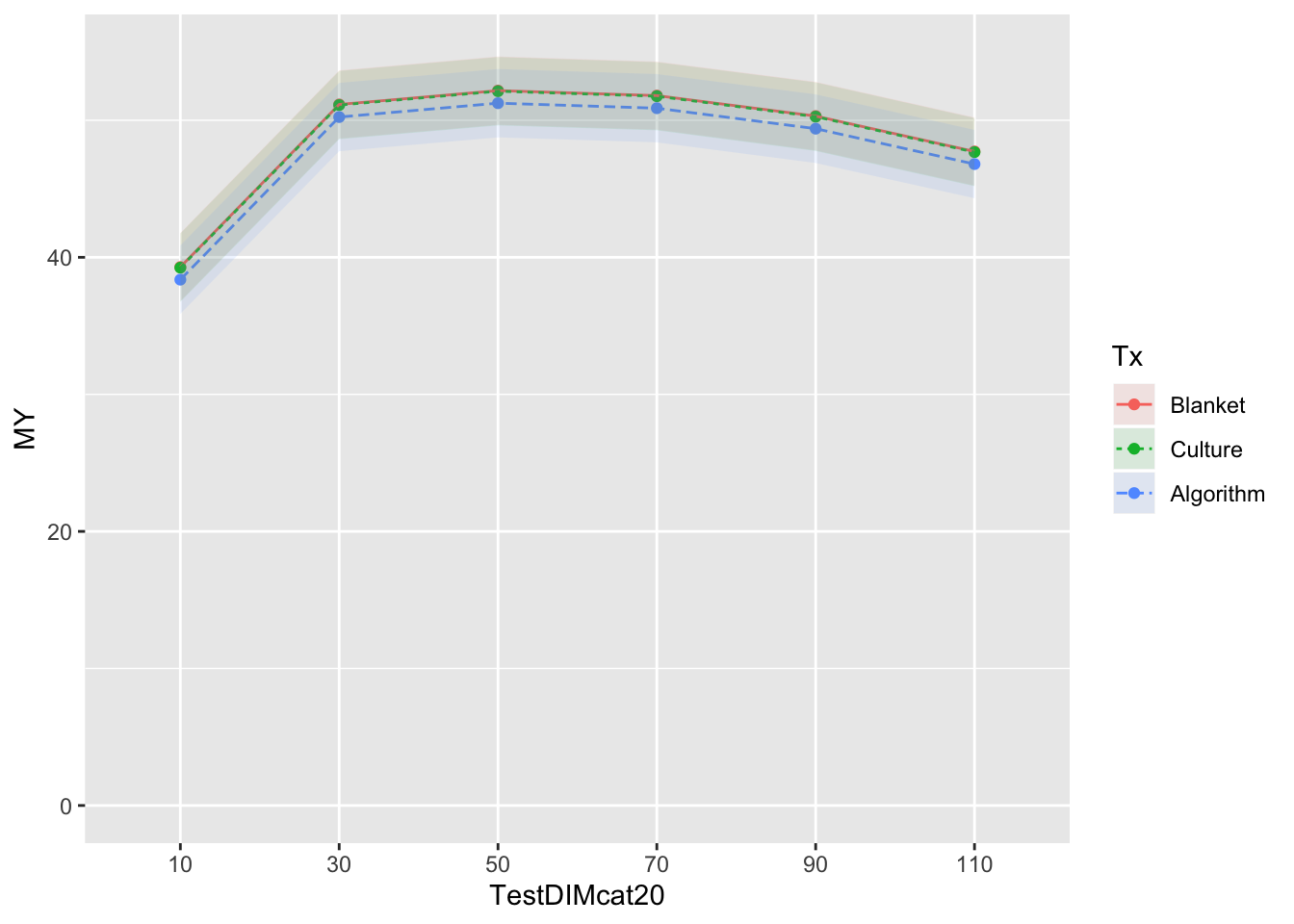





Reported as estimated marginal means by test day category with interaction with herd test DIM

mm0 <- lmer(MY ~ Tx*TestDIMcat20 + Parity + DOMY + (1|FARMID/CowID), data=SDCTCOWDHI)
atx <- c(10,30,50,70,90,110)
emm <- emmeans(mm0, ~Tx*TestDIMcat20, at=list(atx)) %>% tidy()
emm$MY <- emm$estimate
emm$LCL <- emm$asymp.LCL
emm$UCL <- emm$asymp.UCL
emm <- emm %>% subset(select=c(Tx,TestDIMcat20,MY,LCL,UCL))

curve <- ggplot(emm) + coord_cartesian(ylim = (c(0,55))) + aes(x=TestDIMcat20, y=MY, group=Tx, colour=Tx) + geom_point() + geom_line(aes(colour=Tx,linetype=Tx)) + geom_ribbon(aes(ymin=emm$LCL, ymax=emm$UCL,colour=Tx,fill=Tx), linetype=0, alpha=0.1)
curve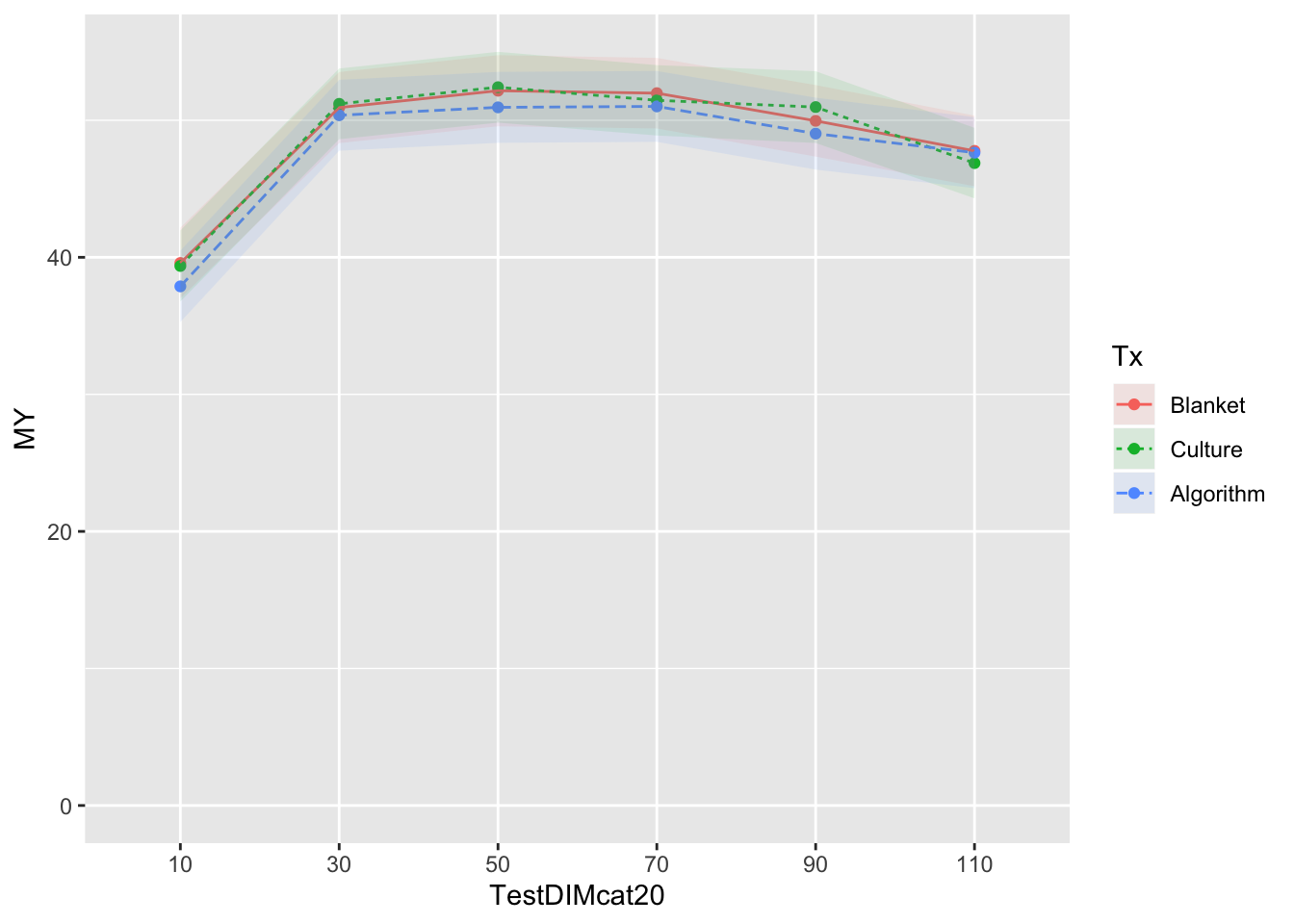

Step 7: Model diagnostics

Checking homoskedasticity assumption (variance of residuals)

mm0 <- lmer(MY ~ Tx + TestDIMcat20 + Parity +DOMY+ (1|FARMID/CowID), data=SDCTCOWDHI)
ggplot(data.frame(eta=predict(mm0,type="link"),pearson=residuals(mm0,type="pearson")),
       aes(x=eta,y=pearson)) +
  geom_point() +
  theme_bw()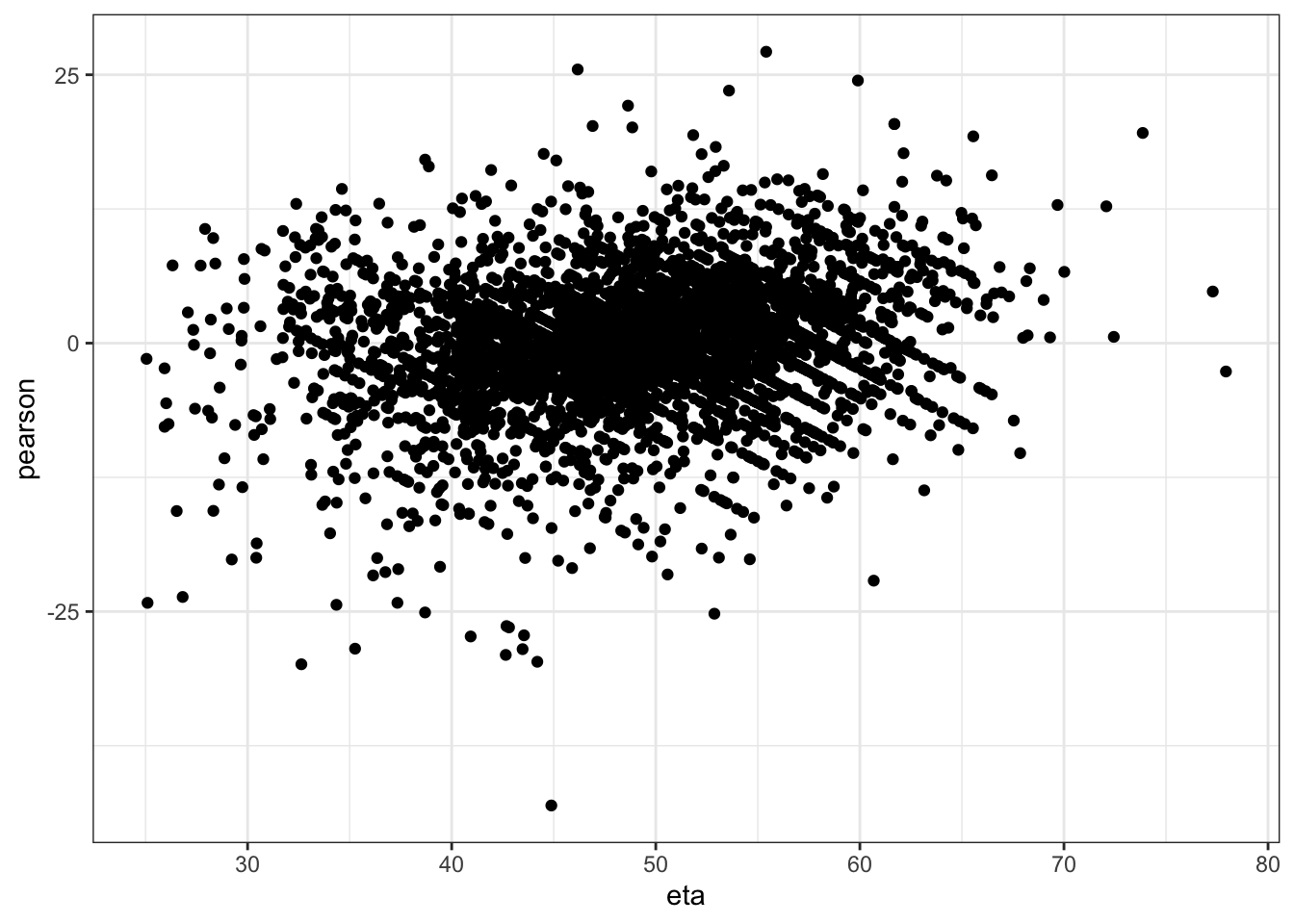

Checking normality of residuals

qqnorm(residuals(mm0))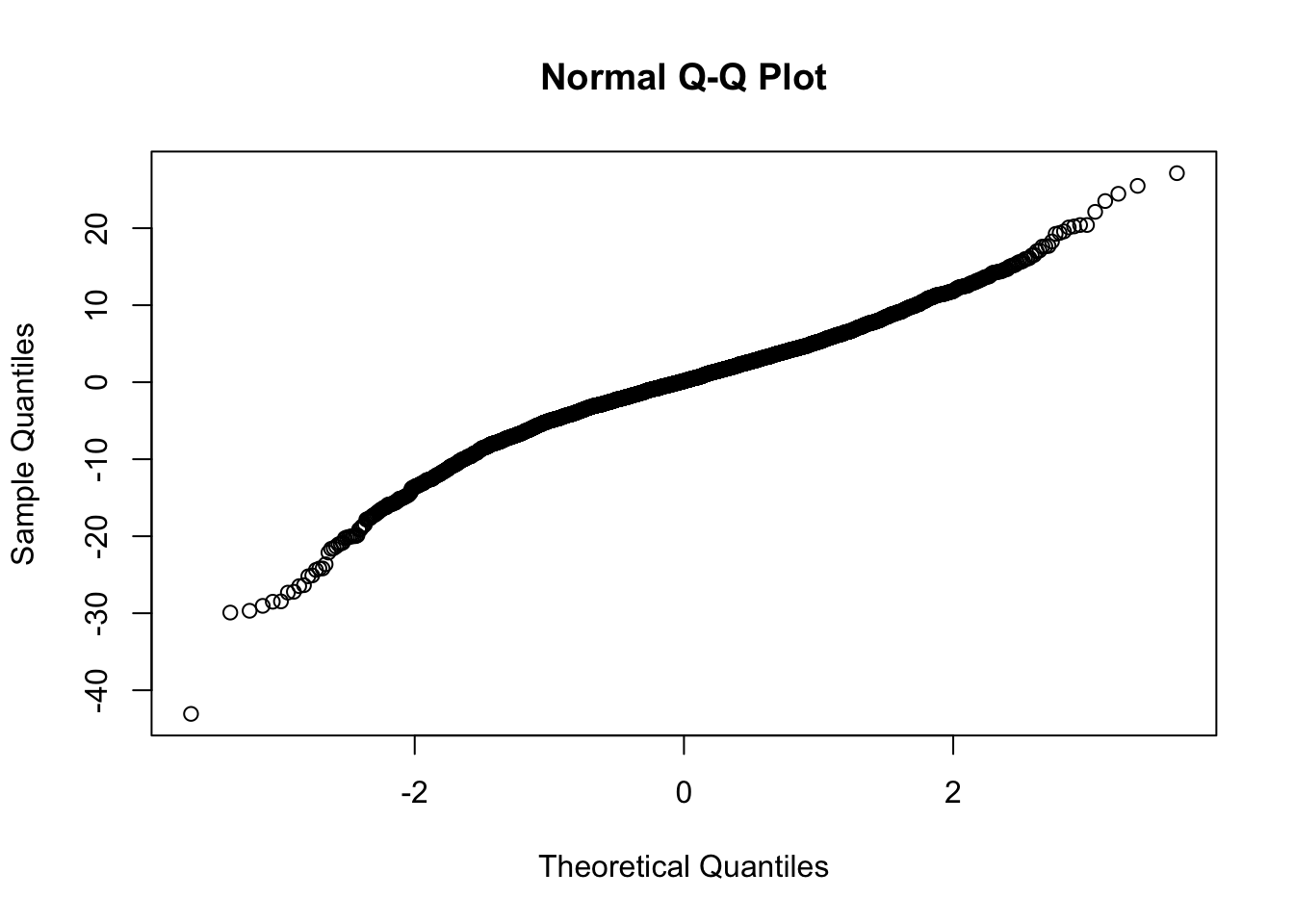

I am happy with homoskedasticity and normal residuals assumptions